Неравенства с модулем. Примеры решения.
Абсолютной величиной (модулем) называется функция, которая каждому числу
х R ставит в соответствие число
R ставит в соответствие число
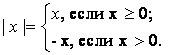
Величина |х| равна расстоянию от точки х до начала координат.
Пусть х и у — действительные числа. Приведем (в виде формул) свойства модуля.
1) |x| 0.
0.
2) |x| = 0 x = 0.
x = 0.
3) |x y| = |x|
y| = |x| |y|.
|y|.
4) |x : y| = |x| : |y|, где у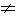 0 .
0 .
5)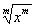 = |x|, где m - четное число (2, 4, 6,...).
= |x|, где m - четное число (2, 4, 6,...).
6) |x|n = xn, где n - четное число (2, 4, 6,...).
7) |x + y| |x| + |y|.
|x| + |y|.
8) |x - y| |x| - |y|.
|x| - |y|.
1. Стандарный способ.
Стандарный способ решения неравенств, содержащих модуль, состоит в том, что, зная промежутки, на которых функция, находящая под знаком модуля принимает значения определенных знаков, снимают знак модуля.
В общем случае при решении неравенств этим способом поступают так:
а) Находят ОДЗ неравенства.
б) Находят точки в которых функции, стоящие под знаком модуля, равны 0.
в) Полученные точки разделяют ОДЗ на несколько множеств.
г) На каждом, из полученных множеств, определяют знак каждой функци и, согласно определению модуля, снимают знак модуля.
д) Решают каждое из полученных неравенств.
е) Полученные множества объединяют.
Задача 1. Решить неравенство |x2 - 3x + 2| + |2x +1| < 5.
Решение.
ОДЗ неравенства R.
x2 - 3x + 2 = 0;
x1 = 1, x2 = 2;
2x + 1 = 0;
x = -0,5;
Три числа -0,5; 1 и 2 разделяют множество действительных чисел на четыре множества. Поэтому рассмотрим четыре случая.
1) (- ; -0,5]. На этом промежутке x2 - 3x + 2 > 0, 2x + 1 < 0,
; -0,5]. На этом промежутке x2 - 3x + 2 > 0, 2x + 1 < 0,
тогда x2 - 3x + 2 -2x - 1 < 5;
x2 - 5x - 4 < 0;
D = 25 + 16 = 41 > 0, следовательно, x1 = ; x1 =
; x1 = ;;
;;
 x
x -0,5,
-0,5, < x <
< x < ;
; Решение этого неравенства на этом промежутке x (
( ; -0,5]
; -0,5]
2) (-0,5; 1]. На этом промежутке x2 - 3x + 2 > 0, 2x + 1 > 0,
тогда x2 - 3x + 2 + 2x + 1 < 5;
x2 - x - 2 < 0;
D = 1 + 8 = 9 > 0, x1 = -1; x2 = 2;
 -0,5< x
-0,5< x 1,
1,-1 < x < 2;
Решение этого неравенства на этом промежутке x (-0,5; 1]
(-0,5; 1]
3) (1; 2]. На этом промежутке x2 - 3x + 2 < 0, 2x + 1 > 0;
-x2 + 3x - 2 + 2x + 1 > 5;
-x2 + 5x - 6 > 0;
x2 - 5x + 6 > 0;
D =25 - 24 = 1 > 0, x1 = 2; x2 = 3;
 1 < x
1 < x 2,
2,x < 2,
x > 3;
Решение этого неравенства на этом промежутке x (1; 2)
(1; 2)
4) (2; + ). . На этом промежутке x2 - 3x + 2 > 0, 2x + 1 > 0;
). . На этом промежутке x2 - 3x + 2 > 0, 2x + 1 > 0;
x2 - 3x + 2 + 2x + 1 < 5;
x2 - x - 2 < 0;
x1 = -1; x2 = 2
 x > 2,
x > 2,-1 < x < 2,
Решение этого неравенства на этом промежутке x
 .
.
Объединим полученные множества ( ; -0,5]
; -0,5] (-0,5; 1]
(-0,5; 1] (1; 2)
(1; 2)
 ;
;
x (
( ; 2).
; 2).
Ответ: ( ; 2).
; 2).
2. Неравенства вида |f(x)| > g(x) ( , <,
, <, ) рекомендуем решать одним из двух способов, которые рассмотрены ниже.
) рекомендуем решать одним из двух способов, которые рассмотрены ниже.
1). Из определения модуля следует, что изучаемые неравенства равносильны совокупности либо системе следующих неравенств:
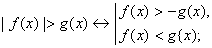
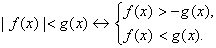
Если неравенства, находящиеся слева от знаков " ", являются нестрогими, то и в правой части зквивалентностей все неравенства следует заменить соответствующими нестрогими ("направленными" в ту же сторону). В частном случае, когда g{х)
", являются нестрогими, то и в правой части зквивалентностей все неравенства следует заменить соответствующими нестрогими ("направленными" в ту же сторону). В частном случае, когда g{х) а = const, неравенствогдеэквивалентно следующему:
а = const, неравенствогдеэквивалентно следующему:
| 1. | |f(x)| < a | a 0 0 | нет решений |
| 2. | |f(x)| < a | a > 0 | -a < f(x) < a |
| 3. | |f(x)| a a | a < 0 | нет решений |
| 4. | |f(x)| a a | a = 0 | f(x) = 0 |
| 5. | |f(x)| a a | a > 0 | -a f(x) f(x) a a |
| 6. | |f(x)| > a | a < 0 | множество решений совпадает с ОДЗ |
| 7. | |f(x)| > a | a = 0 | f(x) 0 0 |
| 8. | |f(x)| > a | a > 0 | f(x) < -a или f(x) > a |
| 9. | |f(x)| a a | a 0 0 | множество решений совпадает с ОДЗ |
| 10. | |f(x)| a a | a > 0 | f(x) -a или f(x) -a или f(x) 0 0 |
Рекомендуем читателю построить график функции y = |f(x)| и обдумать формулы, а заодно и каждую строчку приведенной таблицы.
Пример 2. Решить неравенство |х + 5| > 4.
Решение.
ОДЗ: х R. Согласно восьмой строке таблицы
R. Согласно восьмой строке таблицы
|x + 5| > 4 x + 5 < -4 или x + 5 > 4
x + 5 < -4 или x + 5 > 4 x < -9 или x > -1.
x < -9 или x > -1.
Ответ: х (-
(- ; -9)
; -9) (-1; +
(-1; + ).
).
Пример 3. Решить неравенство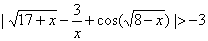 .
.
Решение.
Решим систему неравенств
 17 + x
17 + x 0,
0,8 - x
 0;
0; x
x -17,
-17,x
 8;
8; Таким образом ОДЗ функции, стоящей в левой части неравенства, является множество чисел из промежутка [-17; 0) (0; 8]. На этом множестве левая часть неравенства неотрицательна, следовательно, решением данного неравенства является ОДЗ.
(0; 8]. На этом множестве левая часть неравенства неотрицательна, следовательно, решением данного неравенства является ОДЗ.
Ответ: [-17; 0) (0; 8].
(0; 8].
Пример 4. Решить неравенство |x2 -6x + 5| x + 5.
x + 5.
Решение.
Это неравенство равносильно совокупности неравенств
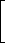 x2 - 6x + 5
x2 - 6x + 5 x + 5,
x + 5,x2 - 6x + 5
 -x - 5;
-x - 5;Упростим каждое из неравенств полученной совокупности
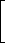 x2 - 7x
x2 - 7x 0,
0,x2 - 5x + 10
 0;
0;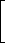 x(х - 7)
x(х - 7) 0,
0,x2 - 5x + 10
 0;
0; Решением первого неравенства является множество чисел (- ; 0]
; 0] [7; +
[7; + ).
).
Квадратный трехчлен x2 - 5x + 10 имеет отрицательный дискриминант, поэтому принимает только положительные значения и, следовательно, второе неравенство решений не имеет.
Ответ: (- ; 0]
; 0] [7; +
[7; + ).
).
2). В ряде случаев (например, если g(х) — квадратный корень либо абсолютная величина, либо любая непрерывная функция, принимающая на всей области определения неотрицательные значения), рассматриваемые неравенства удобнее всего решать возведением в квадрат. Как и в неравенствах |f{x)| > g(х) ( ,
, 1, <), это можно сделать на множестве g(х) > 0. Для тех х из ОДЗ, где g(х) < 0, неравенство проверяется устно. Далее возможен следующий порядок действий (знак ">" выбран для определенности).
1, <), это можно сделать на множестве g(х) > 0. Для тех х из ОДЗ, где g(х) < 0, неравенство проверяется устно. Далее возможен следующий порядок действий (знак ">" выбран для определенности).
Алгоритм решения неравенства|f{x)| > g{х), если g(х) > 0
1.Почленно возвести в квадрат|f(x)|2 > (g(x))2, используя свойство 6, получим неравенство равносильное данному(f{x)2 > (g(х))2
2.Перенести (g{х))2 в левую часть(f(x))2 - {g(x))2 > 0
3.Воспользоваться формулой(f(x) - g(х)) (f(x) + g(x)) > 0
4.Применить метод интервалов
Пример 5. Решить неравенство |x2 - 5x + 9| < |x - 6|.
ОДЗ неравенства R. Так как левая часть неравенства есть модуль от функции, правая часть неравенства есть функция принимающая только положительные значения, то возведем обе части неравенства в квадрат.
|x2 - 5x + 9|2 < |x - 6|2.
(x2 - 5x + 9)2 - (x - 6)2 < 0.
(x2 - 5x + 9 -(x - 6))(x2 - 5x + 9 +(x - 6)) < 0.
(x2 - 6x + 15)(x2 - 4x + 3) < 0.
Дискриминант квадратного трехчлена x2 - 6x + 15 отрицателен (62 - 60 = -24) поэтому на всей области определения он принимает только положительные значения.
Дискриминант квадратного трехчлена x2 - 4x + 3 положителен (42 - 12 = 4), он имеет два корня и они равны 1 и 3. Отрицательные значения квадратный трехчлен принимает, если 1 < х < 3.
Ответ: 1 < x < 3.
3. Способ подстановки.
Введение вспомогательной переменной иногда позволяет намного упростить решение неравенства.
Пример 6. Решить неравенство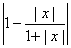

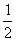 .
.
Решение.
Пусть t = |x|, так как |x| 0, то t
0, то t 0.
0.
Тогда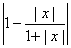

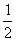 ;
;
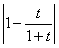

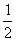 ;
;
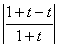

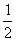 ;
;
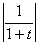

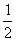 ;
;
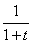

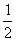 ;
;
t + 1 2; t
2; t 1.
1.
Произведем обратную замену. |x| 1, откуда -1
1, откуда -1 х
х 1.
1.
Ответ: -1 х
х 1.
1.

