Как решать задачи на проценты. Примеры.

  Нахождение процентов от числа  связано с нахождением дроби от числа. Проценты - это особый способ записи обыкновенной дроби, поэтому  начинать раскрывать смысл понятия процентов следует с осмысливания понятия обыкновенной дроби.

  Возьмем несколько обыкновенных дробей, например,. Какой смысл вкладывается в каждую такую запись?
- Это примеры правильных обыкновенных дробей. Знаменвтель каджой из них показывает на сколько равных частей нужно разделить некий реальный или абстрактный объект, числитель показывает сколько таких частей нужно взять. Возьмем в качестве примера какую-нибудь правильную дробь. Например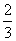. Смысл этого выражения можно раскрыть следующим образом. Некий реальный объект разделили на 3 равные части и взяли из них 2 части.

  В качестве реального объекта можно взять, например, прямоугольник.

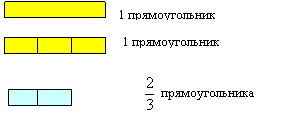
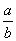 - это выражение представляет собой частное чисел a и b, где b не равно 0.

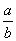 - это отношение чисел a и b, где b не равно 0.

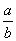 - это обыкновенная дробь. a – числитель, b – знаменатель (b не равно 0).

 Пример 1.  Емкость бочки 200 л.бочки заполнили водой. Какой смысл вложили в это предложение?
- эта дробь означает, что некий объект разделили на 5 равных частей и из них взяли 2 части. Объектом в данной задаче является объем бочки равный 200 л, следовательно,
200:5 = 40,
402 = 80.
В бочку налили 80 литров воды.
Приведенный выше пример это типичный пример на нахождение дроби от числа.

 Теперь можно перейти и к процентам.

 Тогда смысл предложения а% от числа b можно пояснить так. Некий объект (величина, которого равна b единиц) разделили на 100 равных частей и взяли из них a частей.

Пример 2. У Маши было 400 рублей. 24% этой суммы она израсходовала. Какой смысл заключен в этом высказывании?
Так как 24% = 0,24, а 0,24 означает, что некий объект разделили на 100 равных частей и взяли из них 24 части. В данном случае объектом является сумма денег равная 400 руб., следовательно,
400 : 100 =4,
424 = 96.
Маша израсходовала 96 рублей.
Приведенный выше пример это типичный пример на нахождение процентов от числа.

Пример 3. Нужно найти р% от числа b.
Пусть x – число, которое нам нужно найти.
p% = 0,01p,
x = b0,01p

Другой подход к этой задаче. Можно использовать понятие и свойства пропорции. Если вспомнить, что пропорция - это равенство двух отношений, а отношение двух чисел - это обыкновенная дробь, то этот способ также связан с понятием обыкновенной дроби.

b  -   100%,
x   -    р%,
Имеем пропорцию:
b : 100 = x : р,    (b относится к 100 как x относится к p) откуда,

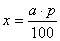
  Пример 4. Пусть имеются числа a и b, причем, a > b Тогда число a больше числа  b   на  %.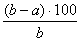

 Подойдем к этой задаче чуть-чуть иначе. Будем рассматривать простой частный случай, например такой: "На сколько процентов число 10 больше числа 2?".

 1. Из большего числа вычитаем меньшее. 10 - 2 = 8. Тогда 10 больше 2 на 8.

 2. Находим отношение, найденного числа к меньшему числу. 8 : 2 = 4 - это отношение двух чисел!

 3 Выражаем отношение в процентах 4100 = 400%.

 Число 10 больше числа 2 на на 400%.

 Если мы 8 разделим на 10 мы найдем отношение, показывающее на какую часть от 10 2 меньше 10 (здесь сравнение идет с числом 10.

 Число 2 меньше числа 10 на 80%.

 Пример 5.  Тракторист вспахал 6 га, что составляетот всего поля. Чему равна площадь всего поля.
Это типичная задача нахождения числа по его дроби.  Пусть площадь всего поля равна x, тогда имеем уравнение x= 6. Откуда x = 6 :;   x = 26. Площадь поля равна 26 га.

 Пример 6. Дано число b, которое составляет p% от числа a. Найти число а.

 p% = 0,01p
b = 0,01pa
a = b : (0,01p)

 Дано число b, которое составляет p% от числа a.

 Найти число а.

  a   -   100%

 b  -    p%

 a : 100 = b : p

  Формула сложных процентов.

Если на вклад положена сумма a денежных единиц, и банк начисляет р% годовых, то через n лет сумма на вкладе составит  денежных единиц, или
a(1+0,01p)ⁿ денежных единиц.

 Пример 7. Постройка дома стоила 9800 рублей, из них 35% заплатили за работу, а остальные деньги за материал. Сколько рублей стоили материалы?

 Решение.

 За работу заплатили:

 35% = 0,35

 0,359800 = 3430.

 Следовательно, материалы стоили: 9800 — 3430 = 6370.

 Ответ: 6370 руб.

 Пример 8. В цистерну налили 37,4 т бензина, после чего осталось незаполненным 6,5% вместимости цистерны. Сколько бензина нужно долить в цистерну для ее заполнения?

 Решение.

 Если незаполненная часть цистерны составляет 6,5% вместимости, то заполненная часть составляет: 100% — 6,5% = 93,5%. Тогда, если х — масса бензина, который осталось долить в цистерну, то имеем пропорцию

 х        -      6,5%

 37,4   -       93,5%,

 откуда.

 Ответ: 2,6 т.

 Пример 9. Найти число, зная, что 25% его равно 45% от 640.

 Решение.

 25%=0,25,

 45%=0,45.

 Пусть х — искомое число. Имеем

 0,25x = 0,45640.

 x = 1152.

 Ответ: 1152.

 Пример 10. Число а составляет 92% от числа b. Если число b увеличить на 700, то новое число будет на 9% больше числа a. Найти числа a и b.

 Решение.

 92%=0б92,

 9%=0,09.

 Из условия задачи имеем систему уравнений:

 Решая полученную систему, находим, а = 230000, b = 250000.

 Ответ: 230000; 250000.

 Пример 11. Первое число составляет 50% от второго. Сколько процентов от первого составляет второе?

 Решение.

 Обозначим второе число через х, тогда первое число равняется 0,5х. Чтобы узнать, сколько процентов составляет число х от числа 0,5x; составим пропорцию:

 0,5х    -    100%,

 х         -     р%,

 из которой находим

 Ответ: 200%.

 Пример 12. В лицее 260 учащихся, из которых 10% неуспевающих. После отчисления некоторого числа неуспевающих, их процент снизился до 6,4%. Сколько учащихся отчислено?

 Решение.

 До отчисления количество неуспевающих до отчисления соляло

 0,1260 = 26.

 Пусть отчислили х человек. Тогда всего в лицее осталось 260 — х учащихся, из них неуспевающих стало 26 - х. Имеем пропорцию

 260 – x       -    100%,

 26 - x              6,4%.

 (260 – x)0,064=(26 - x)100,

 Решая полученное уравнение, находим х = 10.

 Ответ: 10.

 Пример 13. На сколько процентов число 250 превышает число 200?

 Решение.

 Выполним два действия.

 1) Выясняем, сколько процентов составляет число 250 т от числа 200:

 200   -    100%

 250   -     х%

 2) Так как число 200 в данном примере составляет 100%, то число 250 больше числа 200 на 125% -100% = 25%.

 Ответ: 25%.

 Пример 14. На сколько процентов число 200 меньше, чем число 250?

 Решение.

 1) Выясняем, сколько процентов составляет число 200 от числа 250 (в отличие от предыдущего примера, здесь за 100% нужно принимать число 250!):

 250   -   100%

 200   -     х% .

 2) Число 200 меньше числа 250 на 100% - 80% = 20%.

 Ответ: 20%.

 Пример 15. Длину кирпича увеличили на 30%, ширину на 20%, а высоту уменьшили на 40%. Увеличился или уменьшился от этого объем кирпича и на сколько процентов?

 Решение.

 Пусть исходная длина кирпича — х, ширина — у, высота — z. Тогда исходный объем кирпича: V₁ = xyz. Новые размеры кирпича: 1,3х; 1,2у; 0,6z и новый объем: V₂ = 1,3х1,2у0,6z = 0,936xyz. Так как V₂ < V₁, объем кирпича уменьшился. Уменьшение V₂ — V₁ = 0,064xyz и составляет 6,4% от V_1.

 Ответ: уменьшился на 6,4%.

 Пример 16. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

 Решение.

 Обозначим первоначальную цену товара через х. После первого понижения цена станет равной

 х — 0, 4х = 0,6x.

 Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения будем иметь цену

 0,6х - 0,250,6x = 0,45x;.

 После двух понижений суммарное изменение цены составляет:

 х - 0,45x = 0,55х.

 Так как величина 0,55x; составляет 55% от величины x, то цена товара понизилась на 55%.

 Ответ: 55%.

 Пример 17. Первоначальная стоимость единицы продукции равнялась 75 руб. В течение первого года производства она повысилась на некоторое, число процентов, а в течение второго года снизилась (по отношению к повышенной стоимости) на такое же число процентов, в результате чего она стала равна 72 руб. Определите проценты повышения и понижения стоимости единицы продукции.

 Решение.

 Пусть х% - это проценты повышения (и понижения) стоимости единицы продукции. По определению х% от 75 это — 750,01x. Тогда после первого повышения цена станет равняться 75 + 0,75x.

 В течение второго года цена снизится на величину

 0,01x(75+0,75х) = 0,75х + 0,0075х².

 Теперь можно записать уравнение для окончательной цены

 (75 + 0,75х) - (0,75х + 0,0075х²) = 72;

 х² = 400; отсюда x₁ =  - 20, x₂ = 20.

 Подходит только один корень этого уравнения: х₂ = 20.

 Ответ: 20%.

 Пример 18. На банковский счет было положено 10 тыс. руб. После того, как деньги пролежали один год со счета сняли 1 тыс. руб. Еще через год на счету стало 11 тыс. руб. Определить, какой процент годовых начисляет банк.

 Решение.

 Пусть банк начисляет р% годовых.

 1) Сумма в 10000 рублей, положенная на банковский счет под р% годовых, через год возрастет до величины

 10000 + 0,01p10000 = 10000 + 100р руб.

 Когда со счета снимут 1000 руб., там останется 9000 + 100р руб.

 2) Еще через год последняя величина за счет начисления процентов возрастет до величины 9000 + 100р + 0,01p(9000 + 100р) = р² + 190р + 9000 руб.

 По условию эта величина равна 11000 руб, поэтому имеем квадратное уравнение.

 р² + 190р + 9000 = 11000;

 р² + 190р - 2000 = 0
, решим это квадратное уравнение, испрльзуя теорему Виетта, p₁ = 10, p₂ = -200.

 Отрицательный корень не подходит.

 Ответ: 10%.

 Пример 19. В городе в настоящее время 48400 жителей. Известно, что население этого города увеличивается ежегодно на 10%. Сколько жителей было в городе два года назад?

 Решение.

 Предположим, что два года назад количество жителей город было x человек, тогда количество жителей в настоящее время выражается через х по формуле сложных процентов:

 x(1+0,1)² = 1,21x.

 Из условия задачи:

 1,21х = 48400;

 х = 40000.

 Ответ: 40000 человек.