Определение математического понятия.

 Любой объект из окружающего нас мира обладает неким набором свойств. Так, например, конкретная яблоня обладает достаточно большим набором свойств. Вот некоторые из них: имеет корень, ствол, ветви, листья и так далее. Я привел пример хорошо известного большинству из наc объекта. Изучать сразу все свойства объекта трудно. На практике изучают часть свойств реально существующего объекта. Совокупность таких изучаемых свойств называют моделью данного объекта..

В различных науках (физике, математике, химии , биологии и т. д.) изучают свойства реального объекта по его моделям. Эти модели отличаются друг от друга, поскольку различными науками рассматриваются разные его свойства хотя какие-то из них могут совпадать. Математика в этом смысле не исключение, более того, математика вообще оторвалась от реальных объектов, оставаясь крепко связанной с ними.

 Так, например, треугольник обладает такими свойствами: имеет три стороны; три внутренних угла; шесть попарно равных внешних углов и это далеко не все свойства. Математику не интересует, какого цвета треугольник, из какого материала он изготовлен, не ставится задача нахождения массы этого объекта и т.д., перечисленные свойства изучаются другими науками. Более того в природе нет отдельно существующего объекта "треугольник". Если мы вырежем из листа бумаги "треугольник", то с "точки зрения" математики это треугольная призма каждая из двух параллельных граней, которой и есть треугольник. Здесь объект треугольник является частью другого объекта, название которого треугольная призма, но эти объекты не могут существовать друг без друга.

Предложения в которых, что-то утверждается в данный момент являются либо истинными либо ложными, к стати одновременно истинными и ложными они быть не могут. Подобные предложения называются суждениями. Утверждения о наличии или отсутствии у данного объекта какого-либо свойства также называются суждениями.

Вот примеры суждений:

• четырехугольник имеет две диагонали;
• за каждым натуральным числом непосредственно следует в натуральном ряду другое натуральное число
• четное число делится на два и т. д.

Суждениями являются также предложения, указывающие на отношения или связи объектов, например:

• 5 больше 3;
• АВ является стороной треугольника АВС;
• Угол А не является смежным с углом В и т. д.

А вот вопросы, восторги, восхваления, восклицания или требования не являются, суждениями.

Среди свойств какого-либо объекта имеются существенные и несущественные для его определения.

Свойство является существенным, если оно присуще этому объекту и без него он не может существовать. Несущественные свойства, как правило, не влияет на существование объекта. Заметим, что при решении конкретных задач несущественные вообще свойства объектов могут иметь и существенное значение для решения данной задачи.

 Рассмотрим , например, равнобедренный треугольник, изображенный на рисунке. Его свойства: стороны треугольника АВ и АС равны; медиана АD перпендикулярна основанию АD делит угол A пополам - это существенные свойства этого треугольника. А вот свойства: основание ВС равнобедренного треугольника ABC не горизонтально или вершина равнобедренного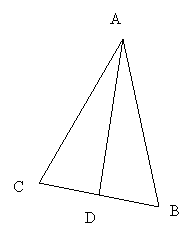треугольника обозначена буквой A - являются несущественными. Мы можем повернуть этот треугольник так, что его основание будет расположено горизонтально и обозначить вершину какой-нибудь другой буквой.  Треугольник от этого не перестанет быть равнобедренным.

 Чтобы иметь представление о каком либо объекте, достаточно знать его существенные свойства. В этом случае говорят, что мы имеем понятие об этом объекте. Следовательно, понятие — это целостная совокупность суждений о существенных свойствах соответствующего объекта. Эта совокупность взаимосвязанных свойств объекта (поэтому она называется целостной) называется содержанием понятия об этом объекте. Заметим, что когда говорят о математическом объекте, то обычно имеют в виду все множество объектов, обозначаемых одним термином (названием).

 Так, когда говорят о математическом объекте — треугольнике, то имеют в виду все геометрические фигуры, являющиеся треугольниками. Множество всех треугольников составляет объем понятия о треугольнике. Точно так же множество всех натуральных чисел составляет объем понятий о натуральном числе. Следовательно, объем понятия — это множество всех объектов, обозначаемых одним и тем же термином. Итак, всякое понятие имеет определенный объем и содержание. Они взаимосвязаны: чем больше объем понятия, тем меньше его содержание, и наоборот: чем меньше объем, тем больше содержание понятия.

Так, например, объем понятия «равнобедренный треугольник» меньше объема понятия «треугольник», ибо в объем первого понятия входят не все треугольники, а лишь равнобедренные. А вот содержание первого понятия, очевидно, больше содержания второго, ибо равнобедренный треугольник обладает не только всеми свойствами треугольника, но и особыми свойствами, присущими только равнобедренным треугольникам.

 В содержание понятия о каком-либо математическом объекте входят много различных существенных свойств этого объекта. Однако, для того чтобы распознать объект, установить, принадлежит ли он к данному понятию или нет, достаточно проверить наличие у него лишь некоторых существенных свойств. Указание этих существенных свойств объекта понятия, которые достаточны для распознавания этого объекта, называется определением понятия.

Всякое определение математического понятия строится обычно так: сначала указывается название объекта этого понятия, затем перечисляются такие его существенные свойства, которые позволяют установить, является ли тот или иной предмет объектом данного понятия или нет.

 Например, определение параллелограмма: «Параллелограммом называется четырехугольник, противоположные стороны которого параллельны». Как видим, это определение построено так: Сначала указано название объекта определяемого понятия — параллелограмм, затем указаны такие его свойства: 1) параллелограмм — это четырехугольник; 2) противоположные стороны параллельны. Первое свойство — это указание того более общего понятия, к которому принадлежит определяемое понятие. Это более общее понятие называется родовым по отношению к определяемому понятию. В данном случае родовым понятием для параллелограмма является четырехугольник. Второе свойство — это указание видового свойства, которое отличает параллелограмм от других видов четырехугольника. Вот еще пример определения: «Четными числами называются такие натуральные числа, которые кратны числу 2». Это определение, так же как и предыдущее, построено по такой схеме:

 В данном случае мы имеем: название определяемого понятия — четные числа, родовое понятие — натуральные числа, видовые отличия — кратны числу 2.

 Определение понятий по этой схеме называется определением через род и видовые отличия.

 Иногда в математике встречаются и другие способы определения понятий. Рассмотрим, например, определение треугольника: «Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков». В этом определении указано родовое понятие для треугольника — фигура, а в качестве видового отличия указан способ построения такой фигуры, которая является треугольником: нужно взять три точки, не лежащие на одной прямой, и соединить каждую их пару отрезком. Такое определение называется генетическим (от слова генезис — происхождение).

 Вот еще пример генетического определения: «Симметрией относительно точки называется такое преобразование фигуры F в фигуру F', при котором каждая точка X фигуры F переходит в точку X' фигуры F', построенной следующим образом: на продолжении отрезка ОХ за точку О откладывается отрезок ОХ', равный ОХ». Здесь в качестве видовых отличий преобразования симметрии относительно точки от других видов преобразований указан способ построения точек фигуры F', симметричной фигуре F относительно точки О.

Встречаются в математике и такие определения, в которых указывается, как можно получить объекты определяемого понятия один за другим по порядку. Например, определение арифметической прогрессии дается таким образом: «Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией». Здесь определяемое понятие — арифметическая прогрессия, родовое понятие — числовая последовательность, в качестве видового отличия указан способ получения всех членов прогрессии, начиная со второго, состоящий в том, что для получения какого-либо члена надо к предшествующему члену прибавить одно и то же число. Это определение можно записать в виде следующей формулы:

a_n = a_n-1 + d, где n ≥2.

 Такое определение называется индуктивным (от слова индукция — наведение на умозаключение от частного к общему) или рекуррентным (от слова рекурсия — возвращение).

 Однако не все математические понятия могут быть логически определены указанными выше способами. Действительно, каждое определение математического понятия сводит определяемое понятие к более широкому (более общему, т. е. имеющему больший объем) родовому понятию, определение родового понятия сводит его к еще более широкому понятию и т. д. Очевидно, что этот процесс сведения одних понятий к более широким, более общим понятиям должен иметь конец, он не может быть бесконечным. Иными словами, в конечном итоге определения понятий мы должны прийти к таким понятиям, которые уже не сводимы к другим, т. е. они логически не определяемы. Такие понятия в математике называются первичными или основными.

 Например, определяя параллелограмм, мы сводим его к понятию четырехугольника, определяя четырехугольник, мы сводим его к понятию многоугольника, затем к понятию геометрической фигуры, которая сводится при определении к понятию точки. Понятие точки уже является не определяемым, т. е. первичным. Первичными понятиями в математике, кроме точки, являются понятия прямой, плоскости, принадлежать, числа, множества, (совокупность) и некоторые другие.

 Овладевая каким либо понятием, необязательно математическим, нужно понимать, что этот процесс сложен и длителен, состоит из нескольких этапов. На начальном этапе нужно произвести анализ свойств изучаемого объекта или его модели, выделить существенные войства и объеденить их в одно множество. Далее происходит длительный процесс запоминания этого множества и привязки его именно к этому объекту. На последнем этапе следует ннаучиться умению строить определение понятий каким-либо способом.

Перейти к следующей странице