Основные свойства неравенств.

  Множество всех действительных чисел можно представить, как объединение трех множеств: множество положительных чисел, множество отрицательных чисел и множество состоящее из одного числа - число нуль. Для того чтобы указать, что число а положительно, пользуются записью а > 0, для указания отрицательного числа используют другую запиь a < 0 .

  Сумма и произведение положительных чисел также являются положительными числами. Если число а отрицательно, то число -а положительно (и наоборот). Для любого положительного числа а найдется такое положительное рациональное число r, что r < а. Эти факты и лежат в основе теории неравенств.

По определению неравенство а > b (или, что то же самое, b < a) имеет место в том и только в том случае, если а - b > 0, т. е. если число а - b положительно.

  Рассмотрим, в частности, неравенство а < 0. Что означает это неравенство? Согласно приведенному выше определению оно означает, что 0 - а > 0, т. е. -а > 0 или, иначе, что число -а положительно. Но это имеет место в том и только в том случае, если число а отрицательно. Итак, неравенство а < 0 означает, что число а отрицательно.

  Часто используется также запись аb (или, что то же самое, bа).
Запись аb, по определению, означает, что либо а > b, либо а = b. Если рассматривать запись аb как неопределенное высказывание, то в обозначениях математической логики можно записать

(a b) [(a > b) V (a = b)]

  Пример 1. Верны ли неравенства 5 0, 0 0?

  Неравенство 5 0 - это сложное высказывание состоящее из двух простых высказываний связанных логической связкой "или" (дизъюнкция). Либо 5 > 0 либо 5 = 0. Первое высказывание 5 > 0 - истинно, второе высказывание 5 = 0 - ложно. По определению дизъюнкции такое сложное высказывание истинно.

  Аналогично обсуждается запись 00.

  Неравенства вида а > b, а < b будем называть строгими, а неравенства вида ab, ab — нестрогими.

  Неравенства а > b и с > d (или а < b и с < d) будем называть неравенствами одинакового смысла, а неравенства а > b и c < d — неравенствами противоположного смысла. Отметим, что эти два термина (неравенства одинакового и противоположного смысла) относятся лишь к форме записи неравенств, а не к самим фактам, выражаемым этими неравенствами. Так, по отношению к неравенству а < b неравенство с < d является неравенством того же смысла, а в записи d > c (означающей то же самое) — неравенством противоположного смысла.

  Наряду с неравенствами вида a > b, ab употребляются так называемые двойные неравенства, т. е. неравенства вида а < с < b,   ас < b, a < cb,
acb. По определению запись

  а < с < b     (1)
означает, что имеют место оба неравенства:

  а < с и с < b.

  Аналогичный смысл имеют неравенства асb, ас < b, а < сb.

  Двойное неравенство (1) можно записать так:

(a < c < b) [(a < c) & (c < b)]

  а двойное неравенство a ≤ c ≤ b можно записать в следующем виде:

(a c b) [(a < c)V(a = c) & (c < b)V(c = b)]

  Перейдем теперь к изложению основных свойств и правил действий над неравенствами, договорившись, что в данной статье буквы a, b, с обозначают действительные числа, а n означает натуральное число.

  1) Если а > b и b > с, то a > с (транзитивность).

 Д о к а з а т е л ь с т в о.

  Так как по условию а > b и b > c, то числа а - b и b - с положительны, и, следовательно, число а — с = (а - b) + (b - с), как сумма положительных чисел, также является положительным. Это означает, по определению, что а > с.

  2) Если а > b, то при любом с имеет место неравенство а + с > b + c.

 Д о к а з а т е л ь с т в о.

  Так как а > b, то число а - b положительно. Следовательно, число               (а + с) - (b + с) = a + c - b - c = а - b также является положительным, т. е.
 a + с > b + с.

  3) Если a + b > c, то a > b - c , т. е. любое слагаемое можно перенести из одной части неравенства в другую, изменив знак этого слагаемого на противоположный.

  Доказательство вытекает из свойства 2) достаточно к обеим частям неравенства а + b > с прибавить число - b.

  4) Если а > b и с > d, то а + с > b + d, т. е. при сложении двух неравенств одного и того же смысла получается неравенство того же смысла.

 Д о к а з а т е л ь с т в о.

  В силу определения неравенства достаточно показать, что разность
(а + с} - (b + c) положительна. Эту разность можно записать следующим образом:
(a + c) - (b + d) = {а - b) + (с - d).
Так как по условию числа а - b и с - d положительны, то (a + с) - (b + d) также есть число положительное.

  Следствие. Из правил 2) и 4) вытекает следующее Правило вычитания неравенств: если а > b, с > d, то a - d > b - с (для доказательства достаточно к обеим частям неравенства а + с > b + d прибавить число - c - d).

  5) Если а > b, то при с > 0 имеем ас > bc, а при с < 0 имеем ас < bc.

  Иначе говоря, при умножении обеих частей неравенства ни положительное число знак неравенства сохраняется (т. е. получается неравенство, того же смысла), а при умножении на отрицательное число знак неравенства меняется на противоположный (т. е. получается неравенство противоположного смысла.

 Д о к а з а т е л ь с т в о.

  Если а > b, то а - b есть число положительное. Следовательно, знак разности ас—bс = с(а — b) совпадает со знаком числа с: если с — положительное число, то и разность ас — bc положительна и потому ас > bс, а если с < 0, то эта разность отрицательна и потому bc — ас положительно, т. е. bc > ас.

  6) Если а > b > 0 и с > d > 0, то ас > bd, т. е. если все члены двух неравенств одинакового смысла положительны, то при почленном умножении этих неравенств получается неравенство того же смысла.

 Д о к а з а т е л ь с т в о.

  Имеем ас - bd = ac - bc + bc - bd = c(a - b) + b{c - d). Так как с > 0, b > 0,         a - b > 0, с - d > 0, то ас - bd > 0, т. е. ас > bd.

  Замечание. Из доказательства видно, что условие d > 0 в формулировке свойства 6) несущественно: для справедливости этого свойства достаточно, чтобы были выполнены условия a > b > 0, с > d, с > 0. Если же (при выполнении неравенств a > b, с > d) числа а, b, с не будут все положительными, то неравенство ас > bd может не выполняться. Например, при а = 2, b =1, c = -2, d = -3 имеем a > b, с > d, но неравенство ас > bd     (т. е.   -4 > -3) не выполнено. Таким образом, требование положительности чисел а, b, с в формулировке свойства 6) существенно.

  7) Если a ≥ b > 0 и c > d > 0, то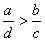(деление неравенств).

 Д о к а з а т е л ь с т в о.

  Имеем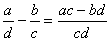Числитель дроби, стоящей в правой части, положителен (см. свойства 5), 6)), знаменатель также положителен. Следовательно,. Этим свойство 7) доказано.

  Замечание. Отметим важный частный случай правила 7), получающийся при а = b  = 1: если с > d > 0, то. Таким образом, если члены неравенства положительны, то при переходе к обратным величинам получаем неравенство противоположного смысла. Предлагаем читателям проверить, что это правило сохраняется и в7) Если ab > 0 и c > d > 0, то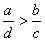(деление неравенств).

 Д о к а з а т е л ь с т в о. то.

  Мы доказали выше несколько свойств неравенств, записанных с помощью знака > (больше). Однако все эти свойства можно было бы формулировать с помощью знака < (меньше), так как неравенство b < а означает, по определению, то же самое, что и неравенство а > b. Кроме того, как это нетрудно проверить, доказанные выше свойства сохраняются и для нестрогих неравенств. Например, свойство 1) для нестрогих неравенств будет иметь следующий вид: если аb и bс, то ас.

  Разумеется, сказанным выше не ограничиваются общие свойства неравенств. Существует еще целый ряд неравенств общего вида, связанных с рассмотрением степенной, показательной, логарифмической и тригонометрических функций. Общий подход для написания такого рода неравенств заключается в следующем. Если некоторая функция у = f(х) монотонно возрастает на отрезке [а, b], то при x₁ > x₂ (где x₁ и x₂ принадлежат этому отрезку) мы имеем f(x₁) > f(x₂). Аналогично, если функция y = f{x) монотонно убывает на отрезке [а, b], то при х₁ > х₂ (где х₁ и х₂ принадлежат этому отрезку) мы имеем f(x₁) < f(x₂). Разумеется, сказанное не отличается от определения монотонности, но для запоминания и написания неравенств этот прием очень удобен.

  Так, например, для любого натурального n функция у = хⁿ является монотонно возрастающей на луче [0, ∞ ). Поэтому мы можем сформулировать следующее общее свойство неравенств:

  8)Если а > b > 0, то aⁿ > bⁿ (где n - натуральное  число).

  Далее, функция y = x²ⁿ⁺¹ является (при любом натуральном n) возрастающей на всей числовой прямой. Иначе говоря, справедливо следующее свойство: a²ⁿ⁺¹ >b²ⁿ⁺¹ ,  тогда когда a > b .

  9) Если а > b, то(где n — натуральное число).

  Отметим один частный случай этого свойства, часто применяемый при доказательстве неравенств (он получается при n = 1) : если а > b, то а³ > b³.

  Наконец, заметим, что если некоторая функция является возрастающей, то и обратная ей функция является возрастающей. Поэтому функция
нa луче [0,) , а функциявозрастает на всей числовой прямой. Это позволяет сформулировать следующие свойства неравенств:

  10)Если а > b > 0, то(где n - натуральное число).

  11)Если а > b, то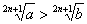(где n — натуралъ ное число).

  Следствие. Неравенство а² > b² имеет место в том и только в том случае, если |а| > |b|.

  В самом деле, если а² > b² то мы можем написать a² > b² > 0, и потому, в силу свойства 10), имеем>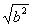т. е. |а| > |b|. Обратно, если |а| > |b|, т. е.>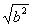, то мы можем написать> 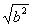 0, и потому, в силу свойства 8),
имеем ()² > (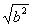}², a² > b².

Еще раз подчеркнем, что рассуждения о монотонности функций, с помощью которых мы написали здесь свойства 8) — 11), не являются доказательствами этих свойств.  Наоборот, лишь после того, как свойство 8) будет доказано, мы можем говорить о монотонности функции у = хⁿ на луче [0, +) (и аналогично для свойства 9)). О доказательстве свойств 8) — 11) мы будем говорить при рассмотрении свойств степенной функции.

  Подобным образом можно написать и ряд друг неравенств.

   Пример 1. Функция у = с^х является при с > 1 возрастающей на всей числовой прямой, то при с > 1 и а > b справедливо неравенство с^a > с^b. Если  0 < с < 1, то при а > b справедливо неравенство с^а < c^b (так   как   при 0 < с < 1 функция у = с^х является убывающей). Об этих неравенствах мы также будем говорить позже.

  Пример 2.  Функция y = log_cx при c >1 является монотонно возрастающей функцией, поэтому при a > b и и c > 1 неравенство log_ca > log_cb справедливо. Эта же функция при 0 < c < 1 монотонно убывает, поэтому при    a > b   и          0 < c < 1 неравенство log_cx  <  log_cx верно.

  Пример 3. Функция y = sinx является на отрезке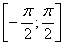монотонно возрастающей, то при а > b, где а и b принадлежат отрезку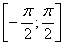, справедливо неравенство sina > sinb.

 
перейти на следующую страницу