Основные правила составления определения понятия.

  Одно и то же математическое понятие может быть определено различными способами. Например, такое простейшее понятие, как «треугольник», в разных учебниках по математике определяется по-разному:

• Треугольник — это замкнутая ломаная линия, состоящая из трех звеньев»;
• Многоугольник, имеющий три стороны, называется треугольником;
• Если А, В и С — любые три точки, не лежащие на одной прямой, то объединение трех отрезков АВ, ВС и АС называется треугольником.

  Все эти определения, как и ранее приведенное, правильные. Однако иногда, воспроизводя определения, имеющиеся в учебнике, или строя определения самостоятельно, ученики и, не только они, допускают разные ошибки. Чтобы строить и воспроизводить определения математических понятий правильно, нужно знать основные требования к логическому определению понятий.

  Рассмотрим эти требования, попутно указывая наиболее часто встречающиеся ошибки в определении математических понятий.

  Определения должны быть научно правильными.

  Это означает, что, определяя то или иное понятие, надо это сделать так, чтобы не исказить научный смысл этого понятия. Так, например, смысл понятия «отношение» (в математике) состоит в том, что оно есть какое-то число. Между тем иногда это понятие определяют так: «Отношение есть сравнение двух чисел или величин посредством деления». Но сравнение есть некоторый процесс, а не число. В данном случае неверно выбрано родовое понятие и тем самым искажен научный смысл определяемого понятия. Другой пример. Иногда приходится слышать от ученика такое определение: «Абсолютной величиной, или модулем числа, называется это число без знака». Получается, что существуют какие-то числа без знака, но таких чисел (кроме нуля) математика не знает: в математике рассматриваются лишь положительные, отрицательные числа и нуль, других чисел нет. Если число написано без знака, то это положительное число, а не какое-то «беззначное». Поэтому приведенное определение неверное.

  Определения не должны содержать «порочного круга».

  Один ученик на вопрос, что такое умножение, например, ответил: «Умножением называется действие отыскания произведения». Когда же его спросили, а что такое произведение, он с уверенностью заявил, что это результат умножения. Следовательно, у этого ученика получается, что умножение определяется через понятие произведения, а произведение через понятие умножения. Получается «порочный круг» в определении. Ясно, что такой способ определения является грубо ошибочным. Еще пример ошибки «порочного круга» в определении: «Угол называется прямым, если его стороны перпендикулярны» и «Прямые называются перпендикулярными, если при пересечении они образуют прямые углы». Схему этих двух определений можно изобразить так.

  Как видим, эти определения действительно образуют «порочный круг». Следовательно, строя определения математических понятий, надо следить за тем, чтобы они не образовали друг с другом «порочного круга».

  Определение должно содержать указание на ближайшее родовое понятие.

  Как бы ни было построено определение математического понятия, в нем должно быть указано ближайшее родовое понятие к определяемому понятию. Нарушение этого требования приводит к различным ошибкам. Так, например, иногда учащиеся, формулируя определения, вовсе не указывают родовое понятие. На вопрос, какие фигуры называется равновеликими, они отвечают: «Это если две фигуры имеют равные площади». Что означает «это», можно лишь догадываться. Или: на предложение сформулировать определение равнобедренных треугольников, иногда можно услышать такой ответ: «Это такие, у которых две стороны равны». Такая небрежность в формулировке определений недопустима. Другой тип ошибок связан с тем, что в определении указывается не ближайшее родовое понятие, а более широкое. Вот пример такого определения: «Параллелограмм есть фигура, у которой противоположные стороны параллельны». В этом определении указано не ближайшее для параллелограмма родовое понятие — «четырехугольник», а более далекое, более широкое — «фигура». И тем самым это определение становится неверным, ибо фигурой, у которой противоположные стороны параллельны, может быть не только параллелограмм, но и, например, правильный шестиугольник. Или другой пример. Давая определение диаметра круга, ученик сформулировал его так: «Диаметр круга есть прямая, проходящая через центр круга». Ученик указал в качестве родового понятия прямую, а ведь диаметр — это не вся прямая, а лишь отрезок прямой.

  Определение не должно быть тавтологией, т. е. повторяющей в иной словесной форме ранее сказанное.

  Сущность такой ошибки заключается в том, что понятие определяется через само себя. Вот примеры тавтологии в некоторых определениях: «Сложением называется действие, при котором числа складываются»(здесь сложение определено через понятие «складывание», что одно и то же). «Фигура А называется симметричной фигуре В, если они расположены симметрично относительно оси симметрии» (здесь «симметричные фигуры» определены через понятие «фигуры, расположенные симметрично»). Ясно, что такие определения являются грубо ошибочными.

  Определение должно быть достаточным.

  Это означает, что в определении должны быть указаны все признаки, позволяющие однозначно выделить объекты определяемого понятия. Если же это требование нарушается, то под определение можно подвести не только объекты определяемого понятия, но и другие объекты. Так, например, иногда ученики дают такое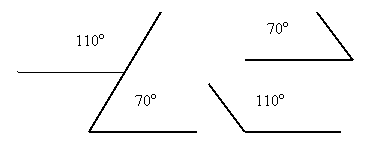определение смежных углов: «Смежными называются углы, которые в сумме составляют 180°». Недостаточность этого определения становится очевидной, если взглянуть на рисунок. На нем изображены две пары углов, сумма которых равна 180°, но они не смежные. Ошибка здесь в том, что указано лишь одно свойство смежных углов, оно недостаточно для их определения. Можно было бы, например, так определить их: «Смежными называются два угла, имеющие общую сторону, которые расположены в разных полуплоскостях от этой общей стороны и в сумме составляют 180°».

  Например, медиану треугольника определили следующим образом: «Медианой треугольника называется отрезок, делящий его сторону пополам». Очевидно, что и в этом определении указано недостаточное число признаков медианы. Поэтому под это определение подходят не только медиана треугольника, но и средняя линия (ведь и она делит сторону треугольника пополам) и вообще любой отрезок, делящий сторону треугольника пополам. Для построения правильного определения медианы треугольника надо добавить еще и такой признак: «Медиана выходит из вершины треугольника». Тогда получаем такое правильное определение: «Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны».

  Определение не должно быть избыточным.

  Это означает, что в определении не должно быть указано лишних признаков, являющихся следствием других признаков определяемого понятия. Например, весьма часто встречается такое определение ромба: «Ромбом называется параллелограмм, все стороны которого равны между собой». Это определение явно избыточное, ибо достаточно равенства двух смежных сторон параллелограмма для того, чтобы были равны все его стороны. Следовательно, правильнее определять ромб следующим образом: «Ромбом называется параллелограмм, две смежные стороны которого равны». Вот другой пример: «Диаметром круга называется наибольшая хорда, проходящая через центр круга». Здесь первый признак «наибольшая» является следствием второго признака «проходящая через центр», а второй является следствием первого. Поэтому правильное определение такое: «Диаметром круга называется хорда, проходящая через центр круга» или: «Диаметром крута называется наибольшая хорда».

  Мы указали лишь основные требования к определению математических понятий и привели примеры ошибок, возникающих при нарушении этих требований. Для того чтобы избежать таких ошибок, надо знать эти требования, учитывать их при формулировании тех или иных определений, учиться строить правильные определения.

Перейти к следующей странице