Основные приемы решения уравнений.

1. Перенос слагаемых из одной части уравнения в другую.

 Переход от уравнения

 f(x) = g(x) + m(x)   (1)
к уравнению

 f(x) - m(x) = g(x)   (2)
называют переносом слагаемых из одной части уравнения в другую.

Перенос слагаемых из одной части уравнения в другую - это преобразование уравнения всегда приводит к равносильному уравнению, т. е., каковы бы ни были функции f(х), m(х), g(x), мы имеем (1)(2).

 В самом деле, пусть a - корень уравнения (1), т. е. соотношение

 f(a) + m(a) = g(a)  = g(a)  + m(a) (3)
представляет собой верное числовое равенство. Это означает, что ринадлежит области определения каждой из функций f{x), m(x), g(x), т. е. определены числа f(a), m(a), g(a), и
2) эти числа связаны соотношением (3).

 Прибавляя к обеим частям равенства (3) число -m(a), получаем
f(a) - m(a)+ m(a) = g(a) - m(a),
или
f(a) = g(a) - m(a) - m(a)  = g(a)   (4)
(поскольку для любого числа b = m(a) верно b - b = 0). Таким образом, (4) есть верное числовое равенство. Но это означает, что a есть корень уравнения (2). Итак, каждый корень уравнения (1) является также корнем уравнения (2), т. е. (1)(2). Аналогично доказывается, что (2)(1). Итак, мы доказали, что при переносе любого слагаемого из одной части уравнения в другую с противоположным знаком получается равносильное уравнение.

  В частности, мы можем, если нужно, перенести все слагаемые в одну часть уравнения. Иначе говоря,

  f(x) = g(x)  f(x) - g(x) = 0

  что является частным случаем эквивалентности (1)(2). Мы видим, что любое уравнение с одним неизвестным можно заменить эквивалентным уравнением вида h(х) = 0, т. е. уравнением, в левой части которого стоит некоторая функция, а правая часть равна нулю. Указанное преобразование (перенос членов из одной части уравнения в другую) применяется при решении уравнений чрезвычайно часто. Например, при решении иррациональных уравнений применяется «уединение радикала», т. е. перенос всех членов, кроме одного, имеющего радикал (корень n-ой степени), в другую часть уравнения.

  Подчеркнем, что в этом пункте шла речь только о перенесении членов из одной части уравнения в другую без последующего приведения подобных членов (если таковые имеются).

  Приведение подобных членов является новым преобразованием (которое может вызвать появление посторонних корней).

2. Приведение подобных членов.

  Переход от уравнения

 f(x) + m(x) - m(x) = g(x)   (5)
к уравнению

 f(x) = g(x)           (6),
называют приведением подобных слагаемых.

  Прежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнеПрежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнение (5) равносильно уравнению

  f(x) + m(x) = g(x) + m(x)   (7).

  Поэтому переход от уравнения (1) к уравнению (2) означает то же самое, что и переход от уравнения (7) к уравнению (2), т. е. во всех рассуждениях уравнение (1) можно заменять равносильным ему уравнением (7). Таким образом, сказанное в этом пункте будет относиться не только к приведению подобных членов в одной части уравнения, но и к вычеркиванию (взаимному уничтожению) одинаковых слагаемых в левой и правой частях. Прежде чем сформулировать общее утверждение, относящееся к переходу от уравнения (1) к уравнению (2) или, что то же самое, от уравнения (7) к уравнению (2), рассмотрим следующие примеры.

  Пример 1.{x⁴ - х + 2}{x² = x}. слагаемого - х и - 2 получается равносильное уравнение х⁴ = х².

 Пример 2.
x² + lgx = x + lgx  х² = х. Уравнение x² = х имеет корня х₁ = 1, х₂ = 0, тогда как уравнение x² + lgx =  x + lgx имеет единственный корень х = 1 (число х = 0 не является корнем уравнения x² + lgx = x + lgx, так при х = 0 левая и правая части этого уравнения не определены). Таким образом, уравнение х² = х не равносильно уравнению х² + lgx = x + lgx, а лишь является следствием этого уравнения. Появление постороннего корня х = 0 при переходе от уравнения x² + lgx = x + lgx к уравнению х² = х связано с тем, что при этом переходе расширяются множества на которых были определены функции, стоящие в левой и правой частях первого уравнения: в уравнении x² + lgx = x + lgx левая и правая части определены при х > 0, а в уравнении х²= х,при всех х. Очевидно, обратный переход, т. е. переход от уравнения х² = х к уравнению х² + lg х = х + lgx вообще недопустим, так как этот переход ведет к потере корня х = 0.

Обозначим через М множество, на котором определены функции f(х) и g(x), стоящие в левой и правой частях уравнения f(x) = g(x) (т.е. пересечение областей определения функций f (х) и g(x). Тогда, если множество М содержится в области определения функции m(х), то уравнение f(x) + m(x) - m(x) = g(x) равносильно уравнению f(x) =g(x). При этих условиях f(x) + m(x) = g(x) + m(x)f(x) = g(x).

3. Умножение обеих частей уравнения на одно и то же выражение.

 Переход от уравнения

  f(x) = g(x)   (8)
к уравнению

  f(x)p(x) = g(x)p(x).   (9)
называют умножением обеих частей уравнения на одно и тоже выражение.

  По поводу этого перехода можно высказать следующие утверждения:

 1) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) (иначе говоря, Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x)), то уравнение (9) является следствием уравнения (8) или (8)(9)

 2) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) и в каждой точке указанного множества функция p(x) отлична от нуля, то уравнения (8) и (9) равносильны, т. е. (8)(9).

  Заметим, что в общем случае переход от уравнения (9) к уравнению (8) может привести как к появлению посторонних корней, так и к потере корней.

  Рассмотрим уравнение x² - x = 0. Умножив обе части этого уравнения на, мы получим уравнение= 0, которое не является следствием исходного. В самом деле, исходное уравнение имеет корни х₁ = 0, х₂ = 1, а уравнение= 0 — лишь корень х = 1. Потеря корня связана с тем, что функция — не определена при. х = 0, а как раз это значение х является корнем заданного уравнения.

  4. Переход от уравнения f₁(x)·f₂(x)·...·f_n(x)  = 0   (*)
к дизъюнкции (совокупности) уравнений
f₁(x) = 0, f₂(x) = 0, ..., f_n(x) = 0,    (**)

  Такой переход применяется довольно часто при решении уравнений. Естественно, возникает вопрос: можно ли утверждать, что уравнение (*) равносильно дизъюнкции уравнений (**)

  Иными словами, можно ли получить «множество всех корней уравнения (*), решив все уравнения (**) и объединив их корни? Ответ на этот вопрос дает следующая теорема.

Теорема 1. Если все функции f_l(x), f₂(x), ..., f_n{x) определены на множестве М (т. е. если множество М содержится в области определения каждой из функций f₁(x), f₂(x), ..., f_n{x)), то на этом множестве уравнение (*) равносильно дизъюнкции уравнений (**).

  Эта теорема лежит в основе часто применяемого метода разложения уравнения на множители.

  Пример 4. x⁶ + 3x⁵ - x⁴ - 3x³ = 0,

  x³(x³ + 3x² - x - 3) =0,

  x³((x³ + 3x²) - (x + 3)) =0,

  x³(x²(x + 3) - (x + 3)) =0,

  x³(x + 3)(x² - 1) =0,

  x³(x + 3)(x - 1)(x + 1) =0.

  Уравнение x⁶ +3x⁵- x⁴ - 3x³ = 0 равносильно дизъюнкции уравнений x³ = 0, x + 3 =0, x + 1 = 0, x - 1 = 0 и имеет следующие корни:

  x₁ = 0, х₂ =1, х₃ = -1, х₄ = -3.

  Следующий пример показывает, что в общем случае уравнение (*) не равносильно дизъюнкции уравнений (**).

  Пример 5. Пусть f₁(х) = х² - 1, f₂(х) =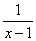. Тогда уравнение f₂(х) = 0 не имеет корней, уравнение f₁(х) = 0 имеет два корня х₁ = 1, х₂ = - 1, а уравнение f₁(х) f₂(х) = 0 имеет только один корень х₁ = -1, так как при х = 1 левая часть этого уравнения не определена.

Теорема 2. Каждый корень уравнения f₁(x)·f₂(x)·...·f_n(x) = 0 является корнем одного из уравнений f₁(x) = 0, f₂(x) = 0,..., f_n(x) = 0.

  Иначе говоря, дизъюнкция уравнений (**) есть следствие уравнения (*). Из этой теоремы вытекает, что если мы найдем все корни уравнений (**), то среди этих корней будут содержаться все корни уравнения (*) и, быть может, некоторые числа, не являющиеся корнями уравнения (*). Посторонними для уравнения (*) будут те значения х, полученные при решении уравнений (**), для которых хотя бы одна из функций f₁(х), f₂(x), ..., f_n(x) не определена.

  3 а м е ч а н и е. Выше было отмечено, что переход от уравнения
f(x)p(x) = g(x)p(x) к уравнению f(x) = g(x) в общем случае недопустим.

  При решении уравнения обычно поступают так. Вместо уравнения
f(x)p(x) = g(x)p(x) рассматривают уравнение (f(x)-g(x))p(x)=0, которое эквивалентно исходному уравнению, т. е. уравнению f(x)p(x) = g(x)p(x).

  В свою очередь дизъюнкция уравнений f(x) - g(x) = 0, p(x) = 0 является следствием уравнения (f(x) - g(x))p(x) = 0. Таким образом, если мы решим уравнения f(x) - g(x) = 0, p(x) = 0, а звтем объединим их корни, и проверкой (подстановкой в уравнение (f(x)p(x) = g(x)p(x) отсеем лишние корни, то тем самым мы найдем все корни искомого уравнения.

  Пример 6. sinx·ctg2x·arcsin(x - 1)·lg(x - 1) = 0.

  Решая каждое уравнение в отдельности, имеем следующее:

  sinx = 0, корни этого уравнения x =k, где kZ;

  ctg2x = 0, корни этого уравнения: x =+pn, где nZ;

  arcsin(x - 1) = 0, корни этого уравнения: x = 1;

  lg(x - 1) = 0, корни этого уравнения: x = 2

  Те из этих корней, которые принадлежат области определения левой части исходного уравнения, являются корнями исходного урапвнения.

 Запишем области определения функций:

  M₁ = D(sinx) = (-; +),

  M₂ = D(ctg2x) = (-; +), x+m, mZ,

  M₃ = D(arcsin(x - 1)) =[0; 2],

  M₄ = D(lg(x - 1)) = (1; +).

  Область определения M левой части исходного уравнения является пересечение множеств M₁, M₂, M₃, M₄.
M = (1;)(; 2]. Из всех найденных корней множеству М, т. е. области определения левой части исходного уравнения, принадлежит корень 2. Корнем исходного уравнения является число 2.

  5. Переход от уравнения f(x)= g(x) к уравнению [f(х)]ⁿ = [g(х)]ⁿ. Такой переход нередко используется при решении уравнений, особенно при решении иррациональных уравнений.

  Пусть функции f(х) и g(x) определены на множестве М (т. е. множество М содержится в области определения каждой из функций f(x), g(x)) и n — произвольное натуральное число. Будем предполагать, что М — некоторое множество действительных чисел и что на этом множестве функции f (х) и g(x) принимают действительные значения. Мы можем утверждать следующее:

1)при любом натуральном n уравнение [f{x)]ⁿ = [g(x)]ⁿ является следствием уравнения f(x) = g{x);
2)если n — нечетное число (n = 2k + 1, то уравнение [f{x)]ⁿ = [g(x)]ⁿ равносильно уравнению f(x) = g{x) на множестве М.
3)если n — четное число, то уравнение [f{x)]ⁿ = [g(x)]ⁿ равносильно на множестве М |f(x)| = |g(x)|, которое в свою очередь равносильно дизъюнкции (совокупности) уравнений f(x) = g(x), f(x) = - g(x) на множестве М. Если при этом окажется, что второе из этих уравнений не имеет решений (например, если обе функции f(x), g(x) принимают на М только положительные значения), уравнение [f{x)]ⁿ = [g(x)]ⁿ равносильно уравнению f(x) = g(x).

  В общем случае переход от уравнения [f(x}]ⁿ = [g(x)]ⁿ к уравнению f(x) = g(x) не допустим, так как такой переход может привести к потере корней.

  Пример 7. Решите уравнение= x + 1.

  Решение. Возводя обе части уравнения в квадрат, получим уравнение

 2x² + 5x - 3 = x² + 2x + 1, являющееся следствием уравнения. Полученное уравнение равносильно уравнению х² + 3х - 4 = 0, корнями которого являются числа х₁ = -4, х₂ = 1. Проверка показывает, что корень x₁ = - 4 является посторонним для уравнения исходного иррационального уравнения, а корень х₂= 1 удовлетворяет уравнению обоим уравнениям. Таким образом, уравнение исходное заданное уравнение имеет единственный корень х = 1.

  Более общим, чем рассмотренный в пятом примере, является переход от уравнения f(x) = g(x) к уравнению m(f(x)) = m(g(x)), где m(t) — некоторая заданная функция. Заметим сразу, что в общем случае такой переход недопустим. В самом деле, пусть Е₁ и Е₂,—множества значений соответственно функций f(x) и g(x) и Е — общая часть (т. е. пересечение) множеств E₁ и Е₂. Если функция m(t) не определена на множестве Е, то уравнение m(f(x)) = m(g(x))не имеет решений, в то время как исходное уравнение могло иметь решения. Если же множество Е содержится в области определения функции m(t), то, как легко доказать, f(x) = g(x)m(f(x)) = m(g(x)). Если же, кроме того, функция m(t) монотонна, то f(x) = g(x) m(f(x) = m(g(x)).

  Пример 8. Уравнение - x⁴ = - x² имеет корни х₁ = 0, x₂ = 1, х₃ = - 1, а уравнение
lg(-х²) = lg(-х⁴) не имеет решений. Произошло это потому, что обе функции
f{x)= -x², g(x) = - x⁴ принимают значения, принадлежащие множеству Е = (-; 0], а на этом множестве функция lgx не определена.

  6. Метод замены неизвестного. Метод замены неизвестного применяется при решении уравнений вида f(g(x)) = 0.

  Он основывается на следующей теореме.

Теорема 3. Рассмотрим уравнение f(t) = 0, где t - вспомогательное неизвестное, и пусть t₁, t₂,₃...,t_k — все корни уравнения. Тогда для решения уравнения f(g(x)) = 0 достаточно найти все корни каждого из уравнений g(x) = t_m (m = l, 2, ..., k) и объединить множества корней этих уравнений.

  Иначе говоря, f(g(x)) = 0g(x) = t₁, g(x) = t₂, ..., g(x) = t_k.

  Эта теорема позволяет свести решение уравнения вида f(g(x))= 0 к решению нескольких более простых уравнений f(t) = 0, g(x) = t_k, где k = 1, 2,..., m.

  Обычно эта теорема применяется следующим образом.

  Дано некоторое уравнение f(x) = 0. Задача заключается в том, чтобы умело подобрать функцию g(x), позволяющую ввести новое неизвестное t = g(x), и затем выразить функцию f(х) через t, т. е. представить ее в виде f(x) = h(g(x)). В результате данное уравнение запишется в виде h(g(x))= 0, и для его решения можно будет применить доказанную теорему. Такой прием решения уравнений и называется методом замены неизвестного (поскольку вначале решается уравнение f(t) = 0, в котором неизвестное х заменено новым, вспомогательным неизвестным t.

  Пример 9. Решить уравнение х² += х -+ 4.

 Решение.

  Введем новое неизвестное t = х -.

  Тогда заданное уравнение примет вид t² - t = 0.

  Уравнение t² - t = 0 имеет корни t₁ = 0, t₂ = 1. Следовательно, х² += х -+ 4х -= 0, х -= 1.

  Решив теперь уравнения

  х -= 0, x₁ =, x₂ = -.

  х -= 1, x₃ = - 1, x₄ = 2.

  Исходное уравнение имеет четыре корня: - 1, -,, 2.

 
перейти на следующую страницу