Информация
Решение задач является наиболее характерной и специфической разновидностью свободного мышления.
Уильям Джемс
Основная часть нашего сознательного мышления связана с решением задач. Когда мы не развлекаемся и не мечтаем, наши мысли направлены к какой-то конечной цели, мы ищем пути и средства к достижению этой цели, мы пытаемся выработать какойто курс, следуя которому, можно достичm конечной цели.
Джордж Пойа
Ни с чем в своей деятельности человек не сталкивается так часто и ни в чем так сильно не нуждается, как в способности ставить и решать задачи самых разнообразных типов и различной степени сложности.
А. Эсаулов
Учимся решать задачу.
Мы установили, что в математике вы должны учиться многим важным умениям, играющим огромную роль в жизни каждого человека, в его работе: строить математические объекты, правильно определять понятия об этих объектах, устанавливать и доказывать существенные свойства этих понятий, проводить их классификацию. Но есть еще одно трудное, но важное умение, которому вам надо научиться,— это умение решать задачи.
Ведь с задачами (житейскими, производственными, научными) человек встречается ежедневно. Любое дело, любая работа в конечном счете сводится к решению задач. Поэтому научиться решать задачи чрезвычайно важно. Конечно, в математике решаются не любые задачи, а лишь математические и сводимые к ним. Но умение решать математические задачи оказывает огромное влияние на общее умение решать задачи, и тот, кто умеет решать эти задачи, сумеет решить и другие.
Решение задач — это сложная работа. Материалом, над которым производится эта работа,— сами задачи, методы их решения — это инструменты для работы, а само решение — это процесс работы, процесс применения инструментов к материалу. Поэтому, чтобы облегчить решение задачи, надо, конечно, знать материал этой работы, т. е. сами задачи — как они устроены, из чего состоят, надо знать и владеть инструментами — методами решения задач, и научиться разумно применять эти инструменты.
Примерами математических задач являются задачи на решение уравнений, неравенств, разные геометрические задачи и т. д. Примерами практических задач являются задачи, в которых речь идет о движении поездов, о работе, о размерах реальных предметов и т. д.
Для сведения практических задач к математическим реальные объекты, рассматриваемые в этих задачах, заменяются соответствующими математическими объектами (числами, отрезками, функциями и т. д.), и тем самым получается модель практической задачи — математическая задача. Приведем пример.
Задача 1. Велосипедист едет из одного города в другой со скоростью 10 км/ч. Если бы он ехал со скоростью 12 км/ч, то приехал бы в город на 4 ч раньше. Каково расстояние между городами?
Для решения этой задачи рассматриваемые в ней реальные объеты - расстояние между городами и скорости велосипедиста заменяем соответственно математическими объектами: х - расстояние между городами и числа 10 и 12 (скорости велосипедиста). Зная, что путь равен произведению скорости на время нахлждения в пути, легко составить уравнение:
Это уравнение и есть модель данной задачи.
Как правило задача содержит несколько условий и одно или несколько требований. В нашей задачи три условия - это скорости велосипедиста и зависимость между временем движения велосипедиста при разных скоростях и одно требование - найти расстояние меду городами.ли более объекта, то указывается соотношение между ними.
Что касается требований, то в математических задачах наиболее часто встречаются такие виды требований:
1) найти искомое (величину, форму, отношение);
2) преобразовать заданный объект в другой вид;
3) построить некоторый объект с заданными характеристиками;
4) доказать справедливость некоторого утверждения.
Задача 2. Разложить на множители многочлен х4 + 4 (1).
В этой задаче имеется одно условие: х4 + 4— многочлен, и одно требование: преобразовать этот многочлен и представить его в виде произведения двух или нескольких многочленов. Это требование второго вида.
Решение этой задачи состоит из следующих шагов.
1. Прибавим к данному многочлену (1) выражение 4х2— 4х2, равное нулю, от этого значение (1) не изменится, получим:
x4 + 4 = x4 + 4 + 4x2 - 4х2.p; (2)
2. Сгруппируем члены (2) следующим образом:
x4 + 4 = x4 + 4 + 4x2 - 4х2 =(x4 + 4x2 + 4) - 4х2. (3)
Это мы имели право сделать на основе переместительного и сочетательного законов сложения.
3. Применим к выражению, стоящему в скобках в правой части (3), формулу квадрата суммы, получим:
(х4 + 4х2 + 4)-4х2 = (х2 + 2)2-4х2. (4)
4. Представим 4x2 как (2х)2, тогда имеем:
(х2 + 2)2-4х2 = (х2 + 2)2-{2х)2. (5)
5. Применим к правой части (5) формулу разности квадратов:
(x2 + 2)2 - (2x)2 = (х2 + 2 + 2х) (х2 + 2 - 2х). (6)
Сопоставим все полученные равенства на основе аксиомы: если а = b и b = с, то а = с, получим окончательно:
х4 + 4 = (x2 + 2 +2x)(x2 + 2 - 2x) (7)
Это решение можно изобразить следующей схемой:
| № шагов | Общие положения математики | Условия | Следствия |
| 1. | a +0 = a | a = x4 + 4 0 = 4x2 - 4x2 | равенство (2) |
| 2. | Переместительный и сочетательный законы сложения | x4+4+4x2-4x2 | равенство (3) |
| 3. | формула: а2+2ab+b2=(a+b)2 | x4+4x2+4 | равенство (4) |
| 4. | Определение степени одночлена | 4x2 = (2x)2 | равенство (5) |
| 5. | формула: a2-b2=(a-b)(a+b) | (x2+2)2-(2x2)2 | равенство (6) |
| 6. | аксиома: если a=b и b=c, то a=c. | равенства (2), (3), (4), (5), (6) | равенство (7) |
Итак, решение любой задачи состоит в том, что находят такую последовательность общих положений математики, применяя которые к условиям задачи или к их следствиям в конечном итоге удовлетворяем требованиям задачи.
Наибольшая трудность в решении задачи — это нахождение указанной последовательности общих положений математики. Если эта последовательность уже найдена, то все остальные в решении — применение этих общих положений к условиям задачи или к следствиям, не представляет большого труда.
Для многих задач в самой математике разработаны эти последовательности общих положений, которые образуют известные общие правила (или, как говорят, алгоритмы) решения задач определенного вида.
Так, например, для производства всех действий над числом имеются готовые правила. Имеются особые правила и для решения многих алгебраических и геометрических задач. Однако большей частью эти правила сформулированы в математике в свернутом виде. Для того чтобы применить их для решения соответствующих задач, вы должны эти свернутые правила развернуть в пошаговую программу.
Например, формула (а + b)2 = а2 + 2ab + b2 есть правило для возведения двучлена в квадрат. Для применения этого правила к решению какой-либо задачи надо это правило развернуть в пошаговую программу. Покажем, как это делается на примере решения задачи:
Представить в виде многочлена выражение (2х— Зу)2.
| 1-й шаг. | Найти в заданном двучлене первый и второй члены | a = 2x, b =3y |
| 2-й шаг. | Возвести первый член в квадрат | a2 = 4x2 |
| 3-й шаг | Найти удвоенное произведение членов двучлена | 2ab = 12xy |
| 4-й шаг | Возвести в квадрат второй член | b2 = 9y2 |
| 5-й шаг. | Сложить результаты 2, 3 и 4-го шагов | 4x2 + 12xy + 9y2 |
Математические задачи, для которых в математике имеются готовые правила - программы их решения, называются, стандартными. Решение стандартных задач особых трудностей не представляет. Надо лишь распознать вид данной задачи, вспомнить соответствующее этому виду задач правило решения, развернуть это правило в пошаговую программу и применить ее к условиям данной задачи.
Значительно труднее решать нестандартные задачи, для которых в математике нет готовых правил. Решение нестандартных задач состоит в том, чтобы свести их к решению одной или нескольких стандартных задач. Например, задача 2 является нестандартной, но мы свели ее к решению нескольких стандартных задач. При поиске способа решения нестандартных задач, при сведении их к стандартным можно пользоваться следующими правилами:
1. Если можно, надо сложную задачу разбить на несколько более простых задач.
Приведем пример разбиения задачи на простые задачи.
Задача 3. Построить график функции: y=|x2-4| + |x|x.
Решение.
Сразу построить график этой функции вряд ли возможно. Попытаемся разбить эту задачу на части - более простые задачи, рассматривая заданную функцию в таких промежутках изменения х, в которых график функции легко построить. Так как в выражение (1) входят модули |x2 - 4| и |x|, то естественно рассмотреть те промежутки, в которых значения выражений стоящих под знаком модуля принимают значения одного знака, т. е. либо положительные значения либо отрицательные. Очевидно, что для этого надо выделить точки, в которых эти выражения меняют свой знак. Этими точками являются числа -2, 0 и 2. Поэтому рассмотрим четыре промежутка:
(- ; -2], (-2; 0], (0; 2], (2; +
; -2], (-2; 0], (0; 2], (2; + ).
).
Тем самым наша задача разбивается на 4 более простые задачи.
1. Построить график функции (1) на промежутке (- ; -2]. На этом промежутке y = (х2 - 4) + (- х)x, y = x2 - 4 - x2, y = - 4. График этой функции будет часть прямой параллельной оси абсцисс.
; -2]. На этом промежутке y = (х2 - 4) + (- х)x, y = x2 - 4 - x2, y = - 4. График этой функции будет часть прямой параллельной оси абсцисс.
2. Построить график функции (1) на промежутке (-2; 0] На этом промежутке у = - (x2- 4) + (-x)x, y = - x2 + 4 - x2, y = - 2x2 + 4. Графиком будет часть параболы, ветви, которой направлены вниз.
3. Построить график функции (1) на промежутке (0; 2]. На этом промежутке у = - (х2 - 4) + хх, y = - x2 + 4 + x 2, y = 4, графиком функции будет прямая параллельная оси абсцисс.
4. Построить график функции (1) на промежутке (2; + ). На этом промежутке y = (x2 - 4) + xx, y = x2 - 4 + x2, y = 2x2 -4, графиком функции является часть параболы, ветви, которой направлены вверх. Таким образом мы полностью построили график функции (1), он состоит, как видим, из четырех частей. В данном случае разбиение сложной задачи на части - более простые задачи, мы произвели, разбив область задачи на части.
). На этом промежутке y = (x2 - 4) + xx, y = x2 - 4 + x2, y = 2x2 -4, графиком функции является часть параболы, ветви, которой направлены вверх. Таким образом мы полностью построили график функции (1), он состоит, как видим, из четырех частей. В данном случае разбиение сложной задачи на части - более простые задачи, мы произвели, разбив область задачи на части.
Иногда разбиение сложной задачи можно производить разбиением условий задачи на части, а иногда можно разбивать на части требование задачи.
Вот пример такой задачи.
Задача 4. При каких значениях а оба корня уравнения х2 - 2ах + 4 = 0 (1) положительны?
Решение.
Для того чтобы оба корня (1) были положительны, нужно, во-первых, чтобы (1) имело два корня, а для этого, как известно, необходимо, чтобы дискриминант уравнения был неотрицательный. Во-вторых, так как свободный член (1) положительный, то оба корня имеют одинаковые знаки, а поэтому, чтобы они имели знаки «плюс», нужно, чтобы коэффициент среднего члена был отрицательный. Следовательно, разбив требование задачи на указанные две части, мы разбиваем и саму задачу на две более простые задачи:
1. При каких значениях а дискриминант уравнения (1) будет неотрицательным? D = a2 - 4. Для того, чтобы D 0, нужно чтобы a
0, нужно чтобы a (-
(- ; -2]
; -2] [2; +
[2; + ). (2)
). (2)
2. При каких значениях а средний коэффициент квадратного уравнения (1) отрицательный? - 2а < 0, отсюда а > 0. a (0;
(0; ) (3)
) (3)
Сопоставляя (2) и (3), получаем окончательно: а [2; +
[2; + ). При этих значениях а оба корня (1) будут положительны.
). При этих значениях а оба корня (1) будут положительны.
3. Если не видно, как решить задачу, то надо попытаться преобразовать ее или заменить другой, равносильной ей.
ПриведПриведем пример.
Задача 5. Решить систему уравнений
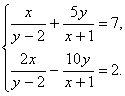
Решение.
Проще всего эту систему решить, заменив ее другой с помощью подстановки:
Тогда исходная система переходит в следующую, ей равносильную:
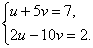
Решив эту систему от относительно u и v, найдем u = 4,
Выполнив обратную замену, подставив вместо u и v их найденные значения, получим новую систему:
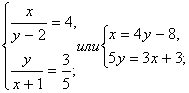
Решив эту систему находим значения x = 4, y = 3. Эта пара чисел будет решением данной в задаче системы.
Задача 6. Расстояние между двумя населенными пунктами А и Б составляет 12 км. Пешеход вышел из пункта А в 9 ч 25 мин и прибыл в пункт Б в 13 ч 15 мин. На следующий день он отправился из пункта Б в обратный путь в 11 ч и пришел в пункт А в 14 ч 40 мин. На каком расстоянии от пункта А находится пункт, который пешеход проходил в один и тот же час как на прямом так и на обратном пути.
Решение.
Обычный способ решения подобных задач - составление уравнений или системы уравнений — в данном случае трудно применить, ибо не видно, как составить уравнение; вопрос задачи уж очень необычный. Проще эту задачу решить, заменяя ее графической моделью.
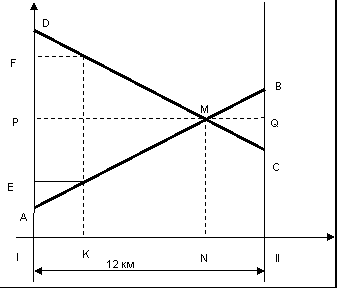
Для этого в системе координат, где на оси абсцисс откладываем в каком-то произвольном масштабе расстояние, а на оси ординат — время в часах и минутах, приэтом за начало на оси времени берем не 0 ч, а 9 ч утра, строим графики движения пешехода туда и обратно (прямые АВ и CD). Если мы возьмем какой-либо пункт на пути пешехода, например пункт К, то этот пункт он проходил на прямом и обратном пути в разное время: на прямом пути в Е ч, а на обратном — в F ч. Но есть один пункт N, который он проходил в одно и то же время как на прямом, так и на обратном пути: этот пункт соответствует точке пересечения графиков его движения — точке М. Это и есть искомый пункт.
Чтобы найти расстояние этого пункта от первого поселка, рассмотрим треугольники AMD и СМВ, они подобны. Поэтому их высоты МР и MQ пропорциональны сторонам AD и СВ. AD = 14 ч 40 мин — 9 ч 25 мин = 5 ч 15 мин = 315 мин, СВ = 13 ч 15 мин — 11 ч — 2 ч 15 мин = 135 мин. Получаем такую пропорцию: PM : MQ = 315 : 135 = 7 : 3. Так как PM + MQ = PQ = 12 км, то находим, что РМ = (7 : 10)· 12 км = 8,4 км.
3. Если данные и искомые (неизвестные) задачи прямо (явно) не связаны, то надо ввести вспомогательные элементы, которые их связывают. Приведем пример использования этой эвристики.
Задача 7. Эту задачу придумал Исаак Ньютон (1643—1727). Трава на лугу растет одинаково густо и быстро. Известно, что 70 коров съели бы всю траву на лугу за 24 дня, а 30 коров — за 60 дней. Сколько коров съедят всю траву на лугу за 96 дней?
Решение.
Непосредственно составить уравнение или систему уравнений по данным задачи нельзя, ибо количество коров и число дней прямо не связаны: они не находятся в прямой или обратной пропорциональности. Чтобы найти связь между ними, введем вспомогательные элементы:
первоначальное количество травы на лугу — а ед.
каждый день там вырастает— b ед.
одна корова за 1 день съедает— с ед.
Теперь можно составить такие уравнения: в первый раз всего травы за 24 дня выросло: а + 246, 70 коров за 24 дня съели 70-24с ед. травы. Тогда по условию а + 246 = 70 -24с.(1)
Аналогично получаем: а + 606 = 30-60с(2)
а + 966= х-96с, где x — искомое количество коров. (3)
Вычитая из (2) почленно (1), найдем: 366 = 120с или с = 0,36. (4) Подставляя значение с из (4) в (1), найдем: а = 4806.(5)
Подставим значения а и с из (5) и (4) в (3), получим: 576b = 28,8x·b. Так как b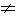 0, то, сократив на b, найдем: х = 20 (коров).
0, то, сократив на b, найдем: х = 20 (коров).
Конечно, при решении многих нестандартных задач приходится использовать не одно какое-либо правило или прием, а несколько. Знание этих правил и приемов, владение ими очень помогает при поиске решения нестандартных задач. Итак, вам надо научиться решать задачи, математические и практические. Для этого прежде всего надо очень внимательно их изучать, анализировать, устанавливать каждый раз условия и требования, содержащиеся в задаче, выяснять, какие объекты, их характеристики и отношения входят в условия, что означают требования задачи. На такой подробный и тщательный анализ не надо жалеть ни времени, ни сил. Только на основе такого анализа будет эффективен ваш поиск способов решения задач. При этом следует помнить, что решение задачи сводится к нахождению таких общих положений математики, применяя которые к условиям задачи или к их следствиям можно удовлетворить ее требования. Поэтому общие положения математики: ее аксиомы, теоремы, правила, формулы, тождества надо знать, надо помнить. Без такого знания вы не сумеете решать задачи. Нахождение способа решения задачи подобно изобретению, а изобретение требует воображения, догадки, фантазии. Поэтому развивайте у себя эти качества. А главное — не спешите при решении задач, не стремитесь решить как можно больше задач. Лучше решить меньше задач, но вдумчиво, с пользой. А для этого, решив задачу, обдумайте проделанное решение, установите, в чем своеобразие задачи, ее решения, что нового вы узнали и приобрели, решив эту задачу. Вот это новое, вот те общие и специальные приемы, которые вы использовали при решении этой задачи, постарайтесь запомнить, усвоить. Все это вам пригодится при решении других задач.

