Равносильные уравнения.

  В процессе решения уравнения мы обычно производим некоторые преобразования, т.е. последовательно заменяем данное уравнение другими уравнениями, все более простыми, пока наконец не получим уравнение, которое мы умеем решать. Трудно перечислить все виды преобразований, которые мы выполняем при решении уравнений: их очень много. Еще труднее дать полный список рекомендаций, в каких случаях следует выполнять те или иные преобразования. Но есть одно непреложное правило, которое никогда не следует забывать: нельзя выполнять преобразования, которые могут привести к потере корней. Ведь мы говорили уже, что решить уравнение - значит найти все его корни, так что потеря корней в процессе решения недопустима.

  Есть и другая опасность, которая может подстерегать нас при решении уравнений, правда, опасность, значительно меньшая, чем потеря корней. Заключается она в том, что при некоторых преобразованиях могут появиться новые корни, т. е. может оказаться, что новое уравнение (к которому мы приходим в результате преобразования) имеет больше корней, чем первоначальное. Иными словами, в новом уравнении, кроме корней первоначального уравнения, могут появиться лишние, посторонние корни. С этим обстоятельством связана необходимость проверки корней. Именно, если хоть один раз в процессе решения применялось преобразование, которое может привести к появлению посторонних корней, то после окончания процесса решения обязательно нужно проверить, какие из найденных корней удовлетворяют исходному уравнению, а какие ему не удовлетворяют, т. е. являются посторонними и, следовательно, должны быть отброшены. Проверку можно не производить только в том случае, если ни одно из примененных преобразований не приводит к появлению посторонних корней.

  Уточним смысл терминов «потеря корней», «посторонний корень».
Пусть g(х) = f(x) заданное уравнение, a f₁(x) = g₁(x) — некоторое новое уравнение, которое мы хотим рассматривать вместо первоначального уравнения (например, уравнение, полученное в результате «преобразования»). Мы говорим, что при переходе от уравнения g(х) = f(x) к уравнению f₁(x) = g₁(x) происходит потеря корней, если существует число х₀ (хотя бы одно), являющееся корнем уравнения f(x) = g(x) и не являющееся корнем уравнения f₁(x) = g₁(x). Далее, число х₁ называется посторонним корнем, получающимся при переходе от уравнения f(x) = g(x) к уравнению f₁(x) = g₁(x), если это число является корнем уравнения; f₁(x) = g₁(x) и не является корнем; первоначального уравнения f(x) = g(x).

  Заметим, что при выполнении таких преобразований, как приведение в уравнении подобных членов, сокращение обеих частей уравнения на общий множитель, отбрасывание общего множителя числителя и знаменателя дроби, могут быть потеряны корни или появятся посторонние корни.

 Рассмотрим несколько простых примеров.

 Пример 1. Если в уравнении x² + 6 += 5x +;

  привести подобные члены, то получится уравнение x² — 5х + 6 = 0, имеющее корни x_l= 2, х₂ = 3. Однако число x_l = 2 не входит в область определения левой и правой частей исходного уравнения и не является его корнем, так как выражение теряет смысл при х = 2. Приведение подобных членов в рассматриваемом примере привело к расширению области определения функций, стоящих в левой и правой частях исходного уравнения, и к появлению корня х = 2, который для исходного уравнения является посторонним.

  Пример 2. Если разделить обе, части уравнения x³ = х на х, то получим уравнение х² = 1, имеющее корни х₁ = 1, х₂ = - 1, в то время как исходное уравнение х³ = х, имеет три корня: x₁ = -1, х₂ = 0, х₃ = 1. Значит, сокращая обе части уравнения на х, мы потеряли корень x = 0.

  Пример 3. Рассмотрим уравнение:

  Если разделить числитель и знаменатель левой части уравнения на sinx, то получится уравнение sin2x = 0,имеющее корни х =n, где n = 0, ±1, ±2, .... Однако исходному уравнению удовлетворяют только те корни уравнения sin 2х = 0, которые удовлетворяют условию sin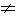х0 (х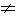k, где k—целое). Таким образом, сокращение числителя и знаменателя левой (или правой) части уравнения на общий множитель может привести к появлению посторонних корней.

 Пример 4. Рассмотрим уравнение: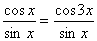

  Отбрасывая знаменатели дробей, приходим к уравнению

 cos х = cosЗх;

  2sinx·sin2x = 0.   (*)

  Так как корни уравнения sinx = 0 удовлетворяют уравнению sin2x = 0, то уравнение (*) имеет те же корни, что и уравнение sin2x = 0, т. е.

 x =n, где n — целое число,(**)

  Однако исходному уравнению удовлетворяют лишь значения х, получаемые из формулы (**) при нечетном n, т. е. х =(2k + 1), k — целое.

  Если же в (**) n - четное (n = 2k), то x =k, sinx = 0; но такие х не входят в область определения левой и правой частей уравнения. Таким образом, отбрасывание знаменателя дроби привело к появлению посторонних корней. Разобранные примеры убеждают в необходимости рассмотрения общей теории уравнений, уяснения влияния тех или иных преобразований на уравнения. Нам потребуется ввести для уравнений понятия равносильности, следствия, дизъюнкции

Определение. Два уравнения f(x) = g(x)   (*)  и  f₁(x) = g₁(x)    (**)
называются равносильными (эквивалентными) на некотором множестве М, если они имеют в этом множестве одни и те же решения, т. е. каждый корень уравнения (*), принадлежащий множеству М, является корнем уравнения (**) и, наоборот, каждый корень уравнения (**), принадлежащий множеству М, является корнем уравнения (*).

  Для сокращения записи равносильные уравнения будем соединять знакомИначе говоря, запись или (*)(**) будет означать, что уравнения (*) и (**) равносильны.

  Замечание. В дальнейшем, если не оговорено противное, под множеством М мы будем понимать множество всех действительных чисел и вместо слов «уравнения равносильны на множестве действительных чисел» будем употреблять слова «уравнения равносильны», т. е. указание на множество М будем опускать.

  Рассмотрим несколько простых примеров, иллюстрирующих определение равносильности.

  Пример 5.    х + 4 = 3хх — 2 = 0.

  Пример 6.   2 cos2 х = 1 + cos 2хх² — 2х = (х— 1)² — 1.

  Любое действительное число является корнем каждого из этих уравнений.

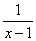  Пример 7.   lgx  =  lg(— х)2 — х += 1 +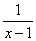

  Пример 8. х+1=0(x + 1)³ = 0.

  Число х = -1 является корнем (простым) первого уравнения и корнем кратности 3 второго уравнения.

  Понятие кратности корня в школьном курсе математики отсутствует. Поэтому мы всюду в этой статье кратность корня не учитываем и два уравнения, имеющие одни и те же корни (без учета кратности), считаются равносильными.

  Пример 9.   Уравнения х² = х  и
не равносильны: число х = 0 является корнем первого уравнения, но не удовлетворяет второму уравнению, так как при х = 0 левая и правая части второго уравнения не определены.

  Пример 10. Уравнения х = 0    и     х(х²+1) = 0
равносильны на множестве действительных чисел (оба имеют единственный корень х = 0) и не равносильны на множестве комплексных чисел, где второе уравнение, кроме корня х₁ = 0, имеет еще два корня: x₂= i, х₃ = -1.

Eсли при решении некоторого уравнения мы заменяем его другим, равносильным уравнением, то, находя корни второго уравнения, мы тем самым найдем корни первоначального уравнения.

  Однако далеко не всегда удается заменить данное уравнение равносильным. Довольно часто, применяя к данному уравнению некоторое преобразование, мы получаем новое уравнение, корнями которого являются все корни данного уравнения и, быть может, некоторые другие числа, не являющиеся корнями данного уравнения. Иными словами, речь идет о преобразованиях, при которых не происходит потери корней; в таких случаях от посторонних корней можно избавиться с помощью проверки.

Определение. Пусть дано некоторое уравнение f(x) = g(x).    (*) и f₁(x) = g₂(x)     (**)
Уравнение (**) называется следствием уравнения (*), если при переходе от уравнения (*) к уравнению (**) не происходит, потери корней, т. е. если все корни уравнения (*) являются корнями уравнения (**).

  Иногда вместо фразы «уравнение (**) является следствием уравнения (*)» используют выражение «уравнение (**) является выводным из уравнения (*)».

  Из приведенного определения следует, что уравнения (*) и (**) равносильны в том и только в том случае, когда каждое из этих уравнений является следствием другого.

  Из определения вытекает также, что уравнение (**), являющееся следствием уравнения (*), может иметь более широкое множество решений, чем множество решений уравнения (*).

  В целях сокращения записи будем использовать знак Þ для обозначения того факта, что второе уравнение (записанное справа от этого знака) является следствием первого. Иначе говоря, запись или (*)(**) означает, что уравнение (**) есть следствие уравнения (*),

  Пример 11. х + 1 = 0х² - 1 = 0.

  Число -1 является единственным корнем первого уравнения, и вместе с тем это число является корнем второго уравнения. Второе уравнение, между прочти, имеет еще один корень, это 1.

   Пример 12. Зx = 2х  + 1sin3x = sin (2х + 1).

  Второе уравнение является следствием первого (обратное неверно, т. е. второе уравнение имеет более широкое множество решений).

Определение. Будем говорить, что уравнение f(x) = g(x)   (*)
равносильно дизъюнкции (совокупности) уравнений
f₁(x) = g₁(x), f₂(x) = g₂(x), ... f_n(x) = g_n(x),    (**)
если выполнены следующие условия:
каждый корень уравнения (*) является корнем по крайней мере одного из уравнений (*);
2) любой корень любого из уравнений (**) является корнем уравнения (*).

  Из этого определения следует, что если уравнение (*) равносильно совокупности уравнений (**) и если М - множество корней уравнения (*), a M_l, М₂, ..., М_п — множества корней соответственно уравнений
f₁(x) = g₁(x), f₂(x) = g₂(x), ..., f_n(x) = g_n(x), то М = M₁M₂...M_n. Иначе говоря, в этом случае вместо того, чтобы решать уравнение (*), можно решить каждое из уравнений (**) в отдельности и множества корней всех этих уравнений объединить. Это объединение и будет представлять собой множество всех корней уравнения (*).

  Тот факт, что уравнение (*) равносильно дизъюнкции (совокупности) уравнений (**), будем записывать следующим образом:
f(x) = g(x)  f₁(x) = g₁(x), f₂(x) = g₂(x),...,f_n(x) = g_n(x),

  в последнее время все чаще используется такая запись:

  Пример 13. x2 - 5х + 6 = 0   x - 2 = 0 и  x - 3 = 0.

  Пример 14. sin²x = cos⁴xsinx - cos²x = 0 и sinх + cos²x = 0.

  Переход от данного уравнения к дизъюнкции более простых уравнений широко применяется при решении уравнений. Как правило, процесс решения уравнения заключается в следующем. Имея уравнение f(x) = g(x), мы (один или несколько раз) применяем переход к новому уравнению или дизъюнкции уравнений, т. е. каждый переход имеет вид f(x) = g(x)f₁(x) = g₁(x), f₂(x) = g₂(x), ..., f_n(x) = g_n(x),

  При этом обязательным является соблюдение следующих правил:

  1) При указанном переходе не происходит потери корней, т. е. если число х₀ есть корень уравнения f(x) = g(x), то это число х₀ должно являться корнем хотя бы одного из уравнений

  f₁(x) = g₁(x), f₂(x) = g₂(x), ..., f_n(x) = g_n(x),

  2)Для решения исходного уравнения f(x) = g(x) нужно решить все уравнения
f₁(x) = g₁(x), f₂(x) = g₂(x), ..., f_n(x) = g_n(x),
и взять объединение множества корней первого из этих уравнений, множества корней второго из этих уравнений и т. д.

  3)Если нет уверенности в том, что не появилось посторонних корней, то каждое число, входящее в это объединенное множество, должно быть, проверено — является оно корнем исходного уравнения или нет. В результате мы и получаем множество всех корней уравнения f(x) = g(x). Если какое-либо из уравнений
f_k(x) = g_k(x) (k = l, 2, ..., не решается непосредственно, то к нему применяется тот же прием.

 
перейти на следующую страницу