Функция.

 Самым общим (и, безусловно, основным) является в математике следующее определение понятия функции.

  Говорят, что определена некоторая функция, если, во-первых, задано некоторое множество, называемое областью определения функции, во-вторых, задано некоторое множество, называемое областью значений функции, и, в-третьих, указано определенное правило, с помощью которого каждому элементу, взятому из области определения, ставится в соответствие некоторый элемент из области значений.

  Приведем несколько примеров, иллюстрирующих это общее определение.

  Пример 1. Обозначим через А множество всех треугольников на плоскости, а через В - множество всех окружностей, взятых на этой же плоскости. Множество А будем считать областью определения, а множество В - областью значений (той функции, которую мы определяем). Наконец, каждому треугольнику поставим в соответствие окружность, вписанную в этот треугольник. Это есть вполне определенное правило, которое каждому элементу, взятому из области определения (т. е. треугольнику), ставит в соответствие некоторый элемент из области значений (т. е. окружность).

  Пример 2. Сохраним те же самые множества А и В, что и в примере 1, т. е. по-прежнему будем считать областью определения множество всех треугольников на плоскости, а областью значений — множество всех окружностей. Далее, каждому треугольнику поставим в соответствие его описанную окружность. Мы получаем функцию с той же областью определения А и той же областью значений В. Но это уже другая функция, так как окружность сопоставляется треугольнику с помощью другого правила.

   Пример 3. Обозначим через К множество всех кругов на плоскости, а через D - множество исех действительных чисел. Далее, выберем единицу измерения площадей и каждому элементу множества К .(т. е. кругу) поставим в соответствие число, равное площади этого крута. Мы получаем функцию с областью определения K и областью значений D.

   Пример 4. Обозначим через N множество всех натуральных чисел, а через R - множество всех действительных чисел. Далее, выберем два действительных числа a и r и каждому натуральному числу n поставим в соответствие действительное число, равное n-му члену арифметической прогрессии с первым членом а и разностью r (т. е. натуральному числу n поставим в соответствие действительное число а + (n - 1)r. Мы получаем функцию с областью определения N и областью значений R.

  Пример 5. Теперь мы примем и в качестве области определения, и в качестве области значений множество R всех действительных чисел. Далее, выберем два действительных числа а и r и каждому действительному числу х поставим в соответствие число а + (х - 1)r. Мы получаем функцию с областью определения R и областью значений R. Заметим, что в примерах 4 и 5 одинакова область значений R и одинаково правило соответствия: формулы    a + (n — 1)r и а + (х — 1)r показывают, что в обоих случаях надо над выбранным числом (n или х) проделать одни и те же действия, чтобы узнать, какое число поставлено ему в соответствие. Однако области определения этих двух функций различны, и потому мы имеем в примерах 4 и 5 разные функции. Таким образом, для задания функции мало указать правило соответствия, а надо еще обязательно указать область определения и область значений.

  Для обoзначения функций обычно пользуются буквами. Одна буква (чаще всего х) используется для обозначения произвольного элемента, взятого из области определения функции. Эта буква называется аргументом. Таким образом, если сказано, что х - аргумент некоторой функции, то вместо х мы можем подставить любой элемент, принадлежащий области определения этой функции. Далее, другая буква (чаще всего у) используется для обозначения произвольного элемента, взятого из области значений. Эта буква называется функцией (и это второе значение слова «функция»). Наконец, третья буква (чаще всего f используется для обозначения правила соответствия. Это значит, что если а - произвольное значение аргумента (т. е. произвольный элемент, взятый из области определения функции), то элемент, поставленный ему в соответствие, обозначается через f(a). Элемент у = f(a) называется значением рассматриваемой функции при х = а. Все три буквы х, у, f объединяются одной записью: y = f{x). («игрек равен эф от икс»), которая и означает, что х — аргумент, y - функция, f -правило соответствия. Иногда букву y или выражение f(х) также называют функцией (и это - уже третье значение слова «функция»).

  Пример 6. Обратимся снова к функции, рассмотренной в примере 4. Аргумент обозначим через n, функцию - через у, а правило соответствия - через f. Таким образом, мы запишем эту функцию в виде y = f(n). Вот несколько значений этой функции:

  f(1) = а₁, f(2) = а₂, где a₂ = a₁ + r и т. д.

  Пример 7. Рассмотрим функцию у = q(х), у которой областью определения и областью значений является множество R всех действительных чисел, а правило соответствия имеет - следующий вид:

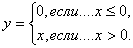
  Вот несколько значений этой функции: q(-15) = 0, q(-23) = 0, q(-1) = 0, q(0) = 0, q(1) = 1, q(3) = 3, q(14) = 14, q(107) = 107, ...

  Разумеется, вместо букв х, у, f можно использовать и другие буквы. Например, запись s = p(t) означает, что s есть функция аргумента t (или короче: s есть функция от t), причем правило соответствия обозначается буквой р.

  Следует подчеркнуть, что область значений функции представляет собой множество элементов (или чисел), среди которых обязательно содержатся все значения рассматриваемой функции. Однако в области значений могут содержаться и «лишние» элементы, не являющиеся значениями функции. Иными словами, множество значений функции обязательно содержится в области значений, но не обязательно совпадает с ней. Так, в примере 3 значениями функции являются лишь положительные числа, тогда как область значений есть множество всех действительных чисел. Несовпадение множества значений функции и области значений можно видеть также в примерах 4 и 7.

  В заключение рассмотрим еще одно (четвертое!) понимание слово «функция», являющееся для школьного курса математики наиболее важным. Именно, функцией называют произвольное выражение, содержащее аргумент х, а также знаки действий и числа.

 Например, функциями (в этом смысле) являются

 y = x² + 2     (2),

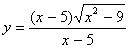    (3),

 y = | 7x - 3 |    (4),

     (5).

 Почему же такие формулы называют «функциями» и не противоречит ли это понимание функции сказанному выше?

 Связь со сказанным выше устанавливается следующим соглашением, которого мы всюду в дальнейшем будем придерживаться:

Если функция задана в виде равенства, в левой части которого стоит у (или другая буква, обозначающая функцию), а в правой части стоит некоторое выражение, содержащее аргумент х или другую букву, а также знаки действия и числа (причем область определения не указана), то принято считать:
1) что за область значений принимается все множество R действительных чисел;
2) за область определения принимается множество всех тех действительных чисел, при подстановке которых вместо х выполнимы (в множестве действительных чисел) все действия, указанные в правой части;
3) если число а принадлежит области определения, то значение функции при  х = а равно числу,  получающемуся, если в правую часть подставить х = а и произвести указанные действия.
Итак, задание функции формулой содержит в себе и указание области определения, и задание правила соответствия.

  Пример 8. Найти область определения функции y = x² + 3.

 Решение.

  В выражении, стоящем в правой части равенства, указан действия возведение в степень и сложение, они выполнимы при любом действительном значении х, т. е. областью определения функции  является все множество D действительных чисел (или, иначе, бесконечный интервал

   (-; +).

  Пример 9. Найти область определения функции.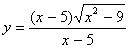

 Решение.

  В выражении, стоящем в правой части равенства, указаны действия: возведение в степень, умножение, сложение, извлечение квадратного корня и деление. Первые три действия всегда выполнимы. Извлечь квадратный корень можно лишь тогда, когда x² - 90, а деление возможно, если x - 5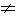0. Так как x² - 90,
при x(-; -3][3;) и x - 5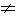0 при x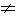5. Учитывая эти рассуждения   область   определения   функции   является   множество чисел

    (-; -3][3; 5)(5; +).

 Пример 10. Найти области определения функций

 Решение.

  Область определения функции состоит  из всех значений х, для которых подкоренное выражение в правой части равенства неотрицательно. Но если выражение - (x- 2)²(x + 4)²(2x - 7)² отлично от нуля, то оно непременно отрицательно. Значит, область определения данной функции состоит лишь из тех точек х для которых подкоренное выражение обращается в нуль. Это будет при х = 2, х = - 4, x = 3,5. Таким образом, область определения данной функции состоит лишь из трех точек: - 4; 2; 3,5.

 Пример 11. Найти область определения функции

  y = f(х) + g(х).

 Решение.

  Пусть функция f(х) определена на множестве М, а функция g(х) на множестве Р. Для того, чтобы некоторая точка х = а принадлежала области определения функции у = f(x) + g (x), необходимо  и  достаточно,  чтобы  при  х = а была определена и функция f(x), и функция g(x). Иными словами, область определения функции y = f(х) + g(х) представляет собой пересечение областей определения функций f(x) и g(x). Исходя из этих соображений Е(у) = М Р.

 Пример 12. Найти область определения функции

 .

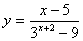 Решение.

  В выражении задающем функцию заданы действия: сложение, возведение в степень и деление. Первые два действия всегда выполнимы во множестве действительных чисел, на 0 делить нельзя, поэтому выясним при каких значениях х выражение 3^x+2- 9 равно 0.
3^x+2 - 9= 0,
3^x+2 = 9,
3^x+2 = 3²
х + 2 = 2,
х = 0.

  Е(у) = (-; 0)(0; +).

  Пример 13. Найти область определения функции y = log₂(2x + 1).

 Решение.

  В выражении задающем функцию заданы действия сложение, умножение и логарифмирование. Первые два действия всегда выполнимы во множестве действительных чисел, логарифм можно, согласно определения логарифма, находить только от положительных чисел, следовательно, чтобы найти область определения данной функции необходимо достаточно решить неравенство

 2х + 1 > 0,

 2х > - 1,

 x > - 0,5.

 E(y) = (- 0,5; +)

 
перейти на следующую страницу