Основные свойства множеств.

  Рассмотрим теперь кратко простые теоретико-множественные понятия и теоретико-множественные операции: пересечение, объединение, дополнение, декартово произведение и др. Для случая конечных множеств они лежат в основе арифметических действий над натуральными числами и поэтому очень важны для школьной математики. Мы ограничимся совсем краткими определениями и пояснениями.

  Множество не содержащее ни одного элемента называют пустым множеством. Его обозначается знаком. Пустое множество можно определить любым противоречивым свойством, например= {х | x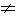х}, в области множеств оно играет как бы роль нуля.

   Множество N называется подмножеством множества М тогда и только тогда, когда каждый элемент множества N принадлежит множеству М. Отношение между множеством М и любым его подмножеством N называется включением и обозначается символом: МN.

  Отметим следующие элементарные утверждения о понятиях подмножества и включения, прямо вытекающих из определения.

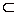  а) Каждое множество М является подмножеством самого себя: ММ. Любое подмножество N множества М, отличное от М, называется собственным подмножеством множества М; соответствующее включение также называется собственным и обозначается: М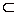N. Принято считать, что пустое множествоявляется подмножеством любого множества М.

  б) Отношение включения транзитивино, т. е. из NМ и РN следует, что РМ. Транзитивно также отношение собственного включения.

  в) Очень важно не смешивать отношения принадлежностии включения: если {а}М, то аМ, и наоборот; но из {a}М не следует {а}М. Так, например, если М = {1, 2}, то это означает, что 1М и 2М, но для всех других объектов х справедливо хМ; для включения же правильны следующие утверждения:

 М, {1}М, {2}М., {1, 2}М.

  Другой пример. Пустое множествоне имеет элементов хM для любого объекта х. Между темсодержит одно подмножество, а именно само себя.

 Введем несколько операций над множествами.

  а) Пересечением множеств М и N называют множество тех объектов, которые принадлежат множествам М и N одновременно.

  Обозначение: МN = {х|хМ и хN}.

  б) Объединением множеств М и N называют множество тех элементов, которые содержатся по крайней мере в одном из множеств М или N. Обозначение: MN = {х | хМ или хN}.

  в) Разностью множеств М и N называют множество тех элементов, которые принадлежат множеству М и не принадлежат множеству N. Обозначение: М \ N. = {х | хМ и хN}.

  г)Симметрической разностью множеств М и N называют множество тех элементов, которые принадлежат только множеству М - или только множеству N.

  Обозначение: MN ={ x | (xМ и хN) или (хN и хМ)}.

  Введенные теоретико-множественные операции наглядно иллюстрируются рисунком 2, где множества М и N изобрансены пересекающимися кругами:

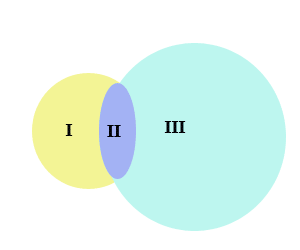
 МN — точки области II;

 МN — точки областей I, II, III;

  М \ N — точки области I;

 N \ М — точки области III;

 MN — точки областей I и III.

 д) В конкретных математических областях бывает полезно ввести в рассмотрение столь обширное множество U, что все рассматриваемые множества окажутся его подмножествами. Такое множество U принято называть универсальным множеством или универсумом. Отметим, что "универсальное множество" понятие относительное: оно выбирается для какого-нибудь определенного раздела науки и притом часто даже явно не определяется, а просто подразумевается.

  Так, например, в элементарной планиметрии в качестве универсального множества принято рассматривать множество всех точек плоскости. Различные фигуры, изучаемые в планиметрии, можно считать множествами точек, т. е. подмножествами так выбранного универсального множества.

  В элементарной арифметике универсальным множеством считается множество Z всех целых рациональных чисел и т. д.

  е) Если выбрано некоторое универсальное множество U, то возникает новая теоретико-множественная операция — дополнение. Для всякого множества М (при этом подразумевается, что М — подмножество универсального множества U его дополнение, обозначаемое через М, — это множество всех элементов универсума, которые не принадлежат множеству М:

  М = {х | хU и xM}

  Таким образом, дополнение — это частный случай разности:

 M = U \ M,
все отличие здесь состоит в том, что разность берется относительно фиксированного множества, содержащего все множества, которые в данной связи рассматриваются.

  Рассмотрим теперь операции декартового произведения множеств. Пусть A и B - два множества. Тогда множество C = {(a, b) | aA, bB}
всех пар (a, b), где a и b независимо друг от друга принимают все значения соответственно из множеств A и B называется декартовым произведением множеств А и В и обозначается через А х В. Если А и В — конечные множества, содержащие соответственно m и n элементов, то сразу видно, что множество А х В содержит mn элементов.

  Самостоятельный интерес представляет тот частный случай, когда множества А и В совпадают: А = В. Чтобы его рассмотреть, вы введем новый термин.

  Упорядоченной парой элементов множества А будем называть объект (а₁, а₂), состоящий из двух (не обязательно различных) элементов а₁, а₂А, с указанием, какой из них следует считать первым, а какой — вторым. Так, например, если А = {1, 2, 3, 4., 5}, то упорядоченные пары (2, 3) и (3, 2) следует считать по определению различными. Упорядоченными парами элементов из А считаются также объекты (1, 1), (2, 2), (3, 3), (4, 4), (5, 5). Упорядоченные пары мы будем заключать в круглые скобки и обозначать жирными строчными латинскими буквами: a = (а₁ а₂), в отличие от неупорядоченных пар, которые, как и множества элементов, записываются в фигурных скобках: {а₁ а₂}.

  Назовем множество

  С = {(а₁, а₂) | a₁А, a₂А}
всех упорядоченных пар (а₁ а₂) элементов из А декартовым квадратом множества А и будем обозначать его через A².

  Рассмотренные свойства множеств и операции над ними в неявном, виде присутствуют в начальном преподавании арифметики. Мы особенно подчеркиваем, что речь идет об их неявном присутствии: бессмысленно было бы в I или II классе давать явные определения арифметических действий. Само слово «действие» для арифметических операций указывает на то, что на начальном уровне развития детей сложение, вычитание, умножение и деление возникают как действия над конкретными множествами из мира, свойственного школьникам. Вековой опыт обучения на всех уровнях показывает, что человек обычно сначала делает нечто, а лишь затем задумывается над тем, какими же общими свойствами обладают его действия.

  Теоретико-множественное обоснование арифметических действий над натуральными числами дается довольно элементарно, так как более строгое обоснование оказывается достаточно трудоемким и мы не имеем возможности провести его здесь со всей необходимой тщательностью. Как мы уже говорили, с точки зрения теории множеств натуральные кардинальные числа отвечают классам равнамощных конечных множеств, к ним, естественно, присоединяется и число нуль как кардинальное число, соответствующее пустому множеству. Тогда элементарные отношения и действия над натуральными числами вводятся следующим образом.

  1.Отношение «равно», «больше», «меньше». Пусть m и n — два натуральных числа и пусть М и N — два множества, кардинальные числа которых суть соответственно m и n. Тогда m меньше n (а n больше m), если множество М равномощно некоторому собственному подмножеству множества N. Как видно из этого же определения, m = n означает, что множества М и N равномощны. Для оправдания такого определения необходимо, конечно, показать, что оно не зависит от выбранных множеств М и N. Иначе говоря, надо доказать, что если М' и N' — два других множества с числом элементов m и n соответственно и если при этом М равномощно собственному подмножеству множества N', то и М' равномощно собственному подмножеству множества N', и наоборот. Это доказательство мы предоставим читателю. Отметим, что определение неравенства для бесконечных кардинальных чисел получается более сложным.

  2.Сложение. Для определения суммы кардинальных чисел поступают так. Пусть m и n — два натуральных числа. Выбираем опять произвольно два непересекающихся множества М с m N с n элементами соответственно, и пусть S — их объединение: S = MN. Тогда по определению сумма s = m + n — это кардинальное число множества S. Покажем, что сумма s от выбора множеств M и N не зависит, а зависит только от их мощностей. Пусть М' и N'— другие множества, равномощные множествам М и N соответственно, и пусть при этом также M'N' =; тогда  S' = М'N' равномощно множеству S = МN. Следует все время иметь в виду, что кардинальное число объединения есть сумма кардинальных чисел объединяемых множеств, только если последние не имеют общих элементов (имеют пустое пересечение). В случае пересекающихся множеств имеет место более общее, правило:

  |MN| = |М| +|N| - |МN|
 (где через |M| обозначается кардинальное число множества M).

  3.Вычитание. Вычитание натуральных чисел поясняется в младших классах на такой модели из теории конечных множеств: пусть m  и n — натуральные числа и пусть М и N — два множества с | М | = m и |N| = n такие, что MN . Тогда d = n - m есть кардинальное число теоретико-множественной разности D |MN| = |М| +|N| - |МN|
 (где через |M| обозначается кардинальное число множества M).ел отвечает образованию декартова произведения множеств. А. именно имеет место разномощность.

 |M x N| = |M||N|

  Так что, если |М| = m и |N| = n, то р = mn - это мощность декартова произведения М х М. Отметим, что Г. Кантор перенес определения арифметических действий и на случай бесконечных кардинальных чисел.