Решение неравенств (метод подстановки).

  Подстановкой в математике называется введение новой переменной. Подстановка позволяет свести решение неравенства или уравнения к двум или нескольким более простым неравенствам или уравнениям. Решая неравенство
f(x) < 0 (>,,), можно сделать подстановку либо в самим неравенстве, либо при решении уравнения f(x) = 0 (третий шаг метода интервалов). Поясним это на примере. Достаточно часто, используя метод постановки, удается понизить степень уравнения или неравенства.

 Пример 1. Решить неравенство х⁴  - х²  -  20.

 Решение 1.

 Пусть t = х². После такой подстановки получится неравенство t² - t - 20, которое мы решим методом интервалов.

  ОДЗ: tR.

  t² - t - 2 = 0,

 t₁ = -1, t₂ = 2.

 f(t) = t² - t - 2; эта функция непрерывна на всей области определения.

 f(3) = 3² - 3 - 2 = 4 > 0;

 Таким образом, функция f(t) = t² - t - 2 - t - 2 - t - 2 принимает  значения небольшие 0, если -1t2. Осуществим обратный переход к переменной x, тогда -1x²2. Это двойное неравенство равносильно системе неравенстви, следовательно,  x[-;].

 Решение 2. Решим неравенство x⁴ - x - 20 методом интервалов.

  ОДЗ: xR.

  Решим биквадратное уравнение х⁴ - x² - 2 = 0.

 Пусть t = x² , t² - t - 2 = 0, отсюда t₁ = - 1, t₂ = 2.

  Производим обратный переход к переменной x.

 x²= -1 (нет корней); x² = 2, x₁ = -, x₂ =.

 Вычисляем значения функции f(x) = x ⁴ - x² - 2,

 f(2) = 2⁴ - 2² -2 >0;

 f(0) = 04 - 02 - 2 < 0;

 f(-2) = (-2)⁴ - (-2)² - 2 >0.

 Таким образом функция f(x) принимает неположительные значения на промежутке [-;].

  Ответ: x[-;].

 Решение 1 дает возможность свести биквадратное неравенство к квадратному
t² - t - 20. Далее решение этого неравенства нужно "перевести с языка t на язык х". В этом и преимущество, и недостаток решения 1. Неравенство сводится к относительно простому, но переход от х к t может вызвать затруднения. Например, если бы t = х +,  то пришлось бы решать систему 

 Решение 2 хорошо тем, что оно дает окончательный ответ. Недостаток этого способа: при решении более сложных примеров есть опасность ошибиться в вычислениях знака функции на интервалах знакопостоянства.

 Пример 2. Решить неравенство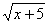7 - x.

 Решение.

 При решении неравенств, содержащих  квадратные корни, необходимо помнить, что возведение в квадрат обеих частей неравенства, сохраняя знак неравенства, можно лишь тогда, когда обе части неравенства принимают неотрицательные значения. Если же обе части неравенства принимают неположительные значения при возведении в квадрат необходимо изменить знак неравенства на противоположный. В перечисленных случаях возможны появления посторонних решений. Возведение неравенства в квадрат в тех случаях, кода части неравенства имеют противоположные знаки, т. е. одна часть принимает неотрицательные значения, а другая неположительные значения может привести к потере решений.  

 Введем вспогательную переменную. Пусть t =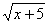, где t0, (из определения квадратного корня)
тогда t² = x + 5; откуда x = t² - 5 и имеем неравенство t7 -  t² + 5;

 t² + t - 120;

  ОДЗ: tR.

 t² + t - 12  = 0;

 t₁ = -4; t₂ = 3.

 f(t) = t² + t - 12; эта функция непрерывна на всей области определения. Формулу, задающую функцию, удобнее записать так f(x) = (x - 3)(x + 4).

 f(4) =4 ² + 4 - 12 = 8 >0;

 Таким образом, функция f(t) = t² + t - 12  принимает  значения небольшие 0, если -4t3. Так как t0, то 0t4. Осуществим обратный переход к переменной x, тогда

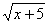
  03. Так как все части неравенства неотрицательны, то возведем их в квадрат 0x + 59, откуда -5x4   и, следовательно, 

  x[-5; 3].

 Ответ: x[-5; 3].

 Пример 3. Решить неравенство 2x² - 8x + 6 >.

 Решение.

 В левой части неравества вынесем 2 за скобки 2(x² - 4x + 3) >и введем вспомогательную переменную.

 Пусть t =, тогда t > 0 и 2t² > t; 2t² - t > 0; t(2t -1) > 0.

 В левой части неравенства задана квадратная функция, в которой старший коэффициент равен 1, а нули 0 и 0,5. Из свойств этой функции следует:

 Таким образом  неравенство 2t² > t равносильно неравенству t > 0,5.

 Выполняем обратную замену переменных.

 > 0,5, где x < 1 или x > 3.

 x² - 4x + 3 > 0,25;

 4x² - 16x + 11 > 0;

 D/4 = 64 - 44 = 20, D > 0.

 x₁ =, x₂ =

 Нетрудно установить, что 0,5 << 1 и 3 << 3,5.

 Таким образом решением исходного неравенства является следующее множество x(-;)(; +).

 Ответ: (-;)(; +).

 Пример 4. Решить неравенство 2sin²x - 3sinx - 2 < 0.

 Решение.

 Пусть sinx = t, где t[-1; 1]    (1), тогда получим квадратное неравенство
2t² - 3t - 2 < 0.

 Для его решения будем использовать свойства квадратной функции.

 1) Её старший коэффициент равен 2.

 2) D = 3² - 42(-2) = 9 + 16 = 25, следовательно, D > 0.

 3) t₁ = -0,5; t₂ = 2, поэтому решением неравенства является множество чисел
t(-; - 0,5)(2; +)    (2).

 Пересечение множеств (1) и (2) есть множество [-1; -0,5).

  Произведем обратный переход к переменной х, получим неравенство.

 -1sinx < -0,5. Для решения этого двойного неравенства воспользуемся свойствами функции y = sinx.

  x(-+ 2k; -+ 2k), где kZ.

 Ответ: x(-+ 2k; -+ 2k), где kZ.

  Пример 5. Решить неравенство 3> lg() + 2.

 Решение.

 Так как -х > 0 при x < 0 и= |x|, где |x| = -x при указанных выще условиях, то заданное неравенство, при x < 0, можно заменить равносильным ему неравенством 3> lg(-x) + 2. Пусть t =, получим квадратное неравенство t² - 3t + 4 < 0.

 1) Старший коээфициент квадратного трехчлена положителен.

 2) Корни квадратного трехчлена: t₁ = 1, t₂ = 2.

 3) Квадратный тречлен принимает отрицательные значения при 1 < t < 2.

  Получаем неравенство 1 << 2. Все три части неравенства положительны, возведем их в квадрат.

 1 < lg(-x) < 4;

 -1000 < x < -10.

 Ответ: (-10000; -10).