Нахождение множества значений функции.

1. Метод оценки (границ).

Для нахождения множества значений функции сначала находят множество значений аргумента, затем, используя свойства неравенств, отыскивают соответствующие наименьше и наибольшее значения функции функции. Если есть возможность путем тождественных преобразований получить функцию, которая на всей области определения или на заранее заданном множестве является непрерывной и либо только возрастающей либо только убывающей, тогда используя свойства неравенств оценивают множество значений  вновь полученной функции.

Пример 1. Найдите множество значений функци y=5 -.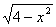

Из определения квадратного корня следует, что 4 - xzbr.gif" class="vr"/> 0, решая квадратичное неравенство получаем, что -2x2. разобьем промежуток [-2; 2] на два промежутка [-2; 0] и (0; 2]. Первому промежутку соответствует неравенство -2x0, а второму соответствует 0 < x2. На первом промежутке переменная х принимает неотрицательные значения, а на втором - положительные.

Возведем в квадрат каждое из этих двойных неравенств, в результате получим 0x²4.
Умножим все три части неравенства на  - 1,  получим неравенство

- 4- x²0.
Прибавим к трем частям неравенства 4 и получим

0  4 - x²  4.
Введем вспомогательную переменную предположив, что

 t = 4 - x², где 0  t4.

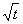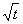
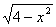
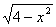
Функция y =на указанном промежутке непрерывна и возрастает, поэтому свои наименьшее и наибольшее значения принимает на концах промежутка и, следовательно, 0   2 тогда произведя обратную замену переменных получим неравенство  0  2. Прибавим к трем частя последнего двойного неравенств 5, умножив его предварительно на - 1, получим 3  5 -  5.

Множество значений функции y = 5 -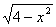является множество [3; 5].

Пример 2. Найти множество значений функции y = 5 - 4sinx.

Из определения синуса следует, -1sinx1. Далее воспользуемся свойствами числовых неравенств.

-4- 4sinx4, (умножили все три части двойного неравенства на -4);

15 - 4sinx9 (прибавили к трем частям двойного неравенства 5);

Так как данная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением на всей области определения, если таковые существуют. В данном случаее множество значений функции y =5 - 4sinxесть множество [1; 9].

Пример 3. Найти множество значений функции y = sinx + cos x.

Преобразуем выражение sinx + cos x  = sinx +sin(- x) =
= 2sin((x  +- x)/2)cos((x ++ x)/2) = 2sin{)cos(x +) =
=cos(x +).

Из определения косинуса следует -1cosx1;

 -1cos(x +}1;

 -cos( x +);

Так какданная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением, если таковые существуют, множество значений функции y =cos(x +) есть множество [-;]. Множество значений  функции

y = sinx + cosx есть множество чисел [-;].

Пример 4. Найти множество значений функции y = 3sinx + 7cos x.

Преобразуем выражение 3sinx + 7cos x. Заметим, что 3² + 7² = 9 + 49 = 58 =Умножим и разделим каждое слагаемое на
3sinx + 7cos x =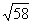(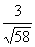sinx +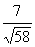cosx).
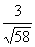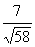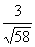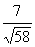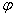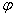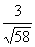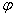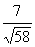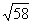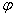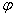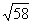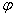Так как< 1 и<  1. и ()² + ()²= 1, то найдется такое числочто cos=и sin=. Тогда 3sinx + 7cos x =(cossinx + sincosx)  =sin(+ x).

Из определения синуса следует, что при любом х справедливо неравенство -1sinx1 и, из периодичности этой функции, следует, что

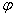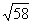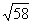
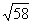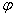-1 sin(+ x) 1, тогда умножая все части двойного неравенства на, имеем -sin(+ x).

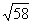Множество значений функции y = 3sinx + 7cos xявляется множество [ -;].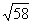

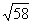2. Метод применения свойств непрерывной функции.

Среди числовых значений, принимаемых на заданном отрезке непрерывной функцией, всегда имеется как наименьшее pначение m, так и наибольшее значение М. Множество значений функции заключено между числами m и M. Это основные утверждения положенны в основу поиска множества значений функции в следующем примере.

Пример 5. Найти множество значений функции y = 2sinx + cos2x на отрезке [0; p].

Решение.

D(y) = R. Данная функция на всей области определения непрерывна, поэтому на отрезке [0; p] существуют такие точки, в которых функция принимает свои наименьше и наибольшее значения. Эти точки либо критические, либо концы отрезка.

1) найдем производную данной функции

2) y' = 2cosx - 2 sin2x = 2cosx - 4sinxcosx = 2cosx(1 - 2sinx)

3) Область определения производной R.

3) Найдем ее критические точки. y' = 0. 2cosx(1 - sinx) = 0, это уравнение равносильно совокупности двух уравнений:
cosx = 0 и 1 - 2sinx = 0.
Решая каждое из них получим:
x =+n, где nZи x = (-1)ⁿ+k, где kZ.

Отрезку [0;] принадлежат три критические точки: x =, x =, x =.

Вычисляем значение функции на концах промежутка и в критических точках:
y(0) = 1, y() = 1, y() = 1,5, y() = 1,5, следовательно, наименьшее значение функции на отрезке[0;] равно 1, а наибольшее значение функции на этом же отрезке равно 1,5. Исходя из выше изложенный утверждений Е(у) = [1; 1,5].

3. Метод приведения к уравнению относительно х с параметром у.

Возможна следующая схема применения этого метода:

Пусть функция задана формулой y = f(x).

2) Рассматриваем функцию как уравнение с параметром у.

3) Выясняем при каких значениях у уравнение f(x) - y = 0 имеет хотя бы один корень. Полученное множество будет множеством значений заданной функции.

Пример 6. найдите множество значений функции.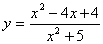

Решение.

x² + 5 > 0 при любом х, следовательно, D(y) = R. Рассматриваем формулу:

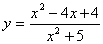, как уравнение с параметром у. Это уравнение равносильно уравнению y(x² + 5) = x² - 4x + 4;

x² (y - 1) + 4x + 5y + 1 = 0;

1) Если у = 1, то данное уравнение равносильно линейному уравнению 4х + 6 = 0, которое имеет один корень.

Если у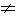1, то квадратное уравнение, которое мы получили в результате выше изложенных соображений, имеет корни тогда и только тогда, когда его дискриминант не отрицателен.

D/4 = 4 - (y - 1)(5y + 1)0;

- 5y² + 4y +50;

5y² - 4y - 50; Вычислим четверть дискриминанта и корни квадратного трехчлена 5y² - 4y -5:

D/4 = 4 + 25 = 29

y = 2 -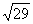и y = 2 +.

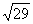Таким образом квадратное уравнение имеет корни,если параметр y[2-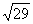; 1) и (1; 2 +],

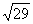Учитывая пункты 1) и 2), делаем вывод, что множество значений изучаемой функции -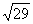 [2 -; 2 +].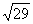

4. Метод непосредственных вычислений.

В случае, когда область определения функции содержит конечное число значений аргумента или  количество значений не велико, или множество значений аргумента может быть описано с помощью конечного числа формул, так бывает в случае рассмотрения тригонометрических функций, обычно множество значений функции находят путем непосредственных вычислений.

Пример 7. Укажите множество значений функции y = 11 -.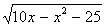

Решение.

Найдем область определения данной функции. Так как в формуле задающей функцию есть квадратный корень, то согласно определению квадратного корня потребуем, чтобы подкоренное выражение было неотрицательным:

10х - х² -250;

-(х - 5)²0;

(х - 5)²0; Откудах = 5. Таким образом область определения данной функции состоит из одного числа, следовательно, множество значений функции состоит из одного числа и Е(у) = {11}.