Учимся доказывать теорему.

  Усвоить содержание теорем (правил, формул, тождеств и т. д.), которые изучаются в школе, не так уж трудно. Для этого необходимо систематически пытаться понять смысл теоремы (правил, формул, тождеств и т. д., как можно чаще применять их при решении задач, при доказательстве других теорем. Такая работа, как показывает практика, приводит к непроизвольному усвоению их содержания, запоминанию их формулировок. Значительно труднее научиться доказывать теоремы. При этом речь идет не о запоминании доказательства той или иной теоремы, которая была рассмотрена на уроке. Специально запоминать доказательство не нужно, нужно научиться самому доказывать теоремы. Доказательства теорем в учебнике следует рассматривать как образец (эталон) рассуждений при доказательстве какого-либо утверждения.

  Что значит доказать теорему, что такое доказательство?

   Доказательство в широком смысле — это логическое рассуждение, в процессе которого истинность какой-либо мысли обосновывается с помощью других положений.

   Поэтому, когда вы убеждаете своего товарища в чем-либо или отстаиваете в споре с ним свое мнение, свою точку зрения, то вы по существу производите доказательство (умело или неумело — это уже другой вопрос) . В жизни все время, каждодневно в общении с другими людьми, приходится доказывать те или иные мысли, утверждения, приходится убеждать в чем-то, т. е. доказывать.

  Доказательство математических теорем есть частный случай доказательства вообще. Оно отличается от доказательства в житейских условиях или в других науках тем, что оно совершается по возможности чисто дедуктивным способом (от латинского слова дедукция — выведение), т. е. выведением новой доказываемой мысли (утверждения, суждения) из ранее доказанных или принятых без доказательства мыслей (аксиом) по правилам логики без каких-либо ссылок на примеры или опыт. В других науках, в житейских обстоятельствах мы для доказательства часто прибегаем к примерам, к опыту. Мы говорим: «Смотри» — и это может служить доказательством. В математике такой способ доказательства недопустим, ссылаться, например, на очевидные отношения, иллюстрируемые чертежом, не разрешается. Математическое доказательство должно представлять собой цепочку логических следствий из исходных аксиом, определений, условий теоремы и ранее доказанных теорем до требуемого заключения.

  Таким образом, при доказательстве теоремы мы сводим ее к ранее доказанным теоремам, а те в свою очередь еще к другим и т. д. Очевидно, что этот процесс сведения должен быть конечным, и поэтому всякое доказательство в конце концов сводит доказываемую теорему к исходным определениям и принятым без доказательства аксиомам.

  Следовательно, аксиомы служат не только для косвенного определения первичных понятий, но и в качестве оснований для доказательства всех теорем математики. Вот почему в числе аксиом встречаются и такие, которые указывают особые свойства понятий, имеющих логические определения. Так, например, параллельные прямые в курсе геометрии являются не первичным понятием, а определяемым. Однако одно из свойств параллельных прямых, а именно что через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной, мы вынуждены принять за аксиому, ибо, как было установлено великим русским геометром Н. И. Лобачевским (1792—1856), а также немецким математиком К. Ф. Гауссом (1777—1855) и венгерским математиком Я. Больяй (1802—1860), доказать это свойство параллельных прямых на основе лишь остальных аксиом геометрии невозможно.

  Всякий шаг доказательства состоит из трех частей:

  1) предложение (аксиома, теорема, определение), на основе которого производится этот шаг доказательства; это основание шага доказательства называется посылкой или аргументом;

  2) логическое рассуждение, в процессе которого посылка применяется к условиям теоремы или к ранее полученным следствиям;

   3) логическое следствие применения посылки к условиям или ранее полученным следствиям.

  В последнем шаге доказательства теоремы в качестве следствия получаем утверждение, которое необходимо было доказать. Покажем процесс доказательства на примере такой теоремы: «Диагонали прямоугольника равны».

  В этой теореме нам дан произвольный (любой) прямоугольник,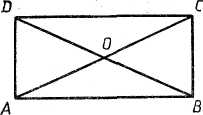Для того чтобы легче было рассуждать в процессе доказательства, поступают следующим образом. Начертим вполне определенный прямоугольник ABCD, но при доказательстве не будем использовать какие-либо частные особенности этого прямоугольника (например, что его сторона АВ примерно в 2 раза больше стороны AD и т. д.). Поэтому наши рассуждения относительно этого определенного прямоугольника будут верны и для любого другого прямоугольника, т. е. они будут иметь общий характер для всех прямоугольников.

  Проведем диагонали АС и BD. Рассмотрим полученные треугольники ABC и ABD. У этих треугольников углы ABC и BAD равны как прямые, катет АВ — общий, а катеты ВС и AD равны как противоположные стороны прямоугольника. Следовательно, эти треугольники равны. Отсюда следует, что стороны АС и BD также равны, что и требовалось доказать.

  Все доказательство этой теоремы можно изобразить в виде следующей схемы.

№ шага	Посылки (аргументы)	Условия	Следствия
1.	Определение: прямоугольник — это четырехугольугольник, у которого все углы прямые	ABCD - прямоугольник	A - прямой B> - прямой.
2.	Теорема: Прямые углы равны.	A - прямой B - прямой.	A =B.
3.	Теорема: Противоположные стороны прямоугольника равны.	ABCD - прямоугольник	BC=AD
4.	Первый признак равенства двух треугольников.	ВС=AD, AB=AB,B =A	ABC=BAD.
5.	Определение равенства треугольников.	ABC =BAD, AC и BD соответственные стороны	AC=BD.

 Самое трудное в доказательстве — это найти последовательность посылок (аксиом, теорем, определений), применяя которые к условиям теоремы или промежуточным результатам (следствиям) в конечном итоге можно получить нужное следствие — доказываемое положение.

  Какими правилами нужно руководствоваться при поиске этой последовательности? Очевидно, что эти правила не могут носить обязательный характер, они лишь указывают возможные пути поиска. Поэтому они называются эвристическими правилами или просто эвристиками (от греческого слова эврика — нахожу, нашел). Многие выдающиеся математики, такие, как Папп (древнегреческий математик, живший в III в.), Блез Паскаль (1623—1662), Рене Декарт (1596—1650), Жак Адамар (1865—1963), Дьердж Пойя (1887) и многие другие, занимались разработкой эвристик для поиска доказательства теорем и решения задач. Вот некоторые эвристические правила, которые полезно помнить:

  1.Полезно заменять названия объектов, о которых идет речь в теореме (задаче), их определениями или признаками.

  Например, в рассмотренной выше теореме шла речь о прямоугольнике, и мы для доказательства использовали определение прямоугольника.

  2.Если можно, то нужно доказываемое положение раздробить на части и доказывать каждую часть в отдельности.

  Так, например, доказательство теоремы: «Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм» — можно разделить на две части: сначала доказать, что одна пара противоположных сторон данного четырехугольника параллельна, а затем доказать, что и вторая пара противоположных сторон также параллельна.

  Так следует поступать всегда, когда есть возможность доказываемое утверждение разбить на несколько частей более простых утверждений.

  3.В поисках доказательства теоремы полезно идти с двух сторон: от условий теоремы к заключению и от заключения к условиям.

  Например, нужно доказать такую теорему: «Если некоторая последовательность такова, что любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, то эта последовательность — арифметическая прогрессия».

  Пойдем от условия теоремы. Что нам дано? Дано, что каждый член последовательности, начиная со второго (обозначим его a_n, где n³2), есть среднее арифметическое предшествующего и последующего членов, т.

  a_n-1 и a_n+1. Значит, верно такое равенство:
     (1)

  Теперь пойдем от заключения. А что нам нужно доказать? Нужно доказать, что эта последовательность — арифметическая прогрессия. А какая последовательность называется арифметической прогрессией? Вспоминаем определение:

  a_n = a_n-1 + d, где n2, d — постоянное число.            (2)

  Сопоставляем данное нам условие (1) с заключением (2). Чтобы условие приняло форму заключения, надо преобразовать так:

   2a_n = a_n-1 +  a_n+1,                                         (3)

  Отсюда a_n — a_n-1 = a_n+1 — a_n.                      (4)

  Левая и правая части (4) обозначают одно и то же, а именно разность между двумя последовательными членами заданной последовательности. Если в равенстве (4) п давать последовательно значения 2, 3 и т. д., то получим: а₂ —a₁ = а₃ — a₂,  затем       а₃ - a₂ = a₄ - a₃ и т. д. Следовательно, все эти разности равны между собой, а это значит, что разность а_п — а_п-1  есть постоянное число, которое можно обозначить буквой, например, буквой  d:

  а_п — а_п-1 = d.

  Отсюда получаем: a_n = a_n-1 + d, а это значит, что согласно определению (2) данная последовательность есть арифметическая прогрессия, что нам и надо было доказать.

  Эту эвристику можно и так сформулировать: надо стараться сблизить условие и заключение теоремы, преобразуя их или заменяя их следствиями.

  Известен и ряд более частных эвристических правил, которые применяются при поиске лишь некоторых теорем. Например, такая эвристика: для того чтобы доказать равенство каких-либо отрезков, надо найти или построить фигуры, соответствующими сторонами которых являются эти отрезки; если фигуры окажутся равными, то будут равны и соответствующие отрезки.

  Изучая теоремы, нужно не просто запоминать их доказательство, а каждый раз думать и устанавливать, какими методами они доказываются, какими эвристическими правилами руководствовались при нахождении этих доказательств, как догадались (додумались) до этих доказательств.

  В ряде случаев для доказательства теорем используется особый прием, называемый «доказательством от противного» или «приведением к нелепости».

  Сущность этого приема заключается в том, что предполагают несправедливость (ложность) заключения данной теоремы и доказывают, что такое предположение приводит к противоречию с условием или с ранее доказанными теоремами или аксиомами. А так как любое утверждение может быть либо верным, либо неверным (ничего другого быть не может), то полученное противоречие показывает, что допущение о ложности заключения теоремы неверно и, следовательно, заключение верно, тем самым теорема доказана.

  Приведем пример.

  Теорема. Две прямые, порознь параллельные третьей, параллельны между собой.

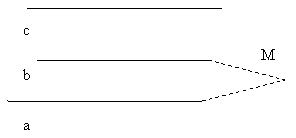
    Дано: а||с, b||с.  
    Доказать: а||b.

  Докажем эту теорему методом от противного. Допустим, что заключение теомы неверно, т. е. прямая а непараллельна прямой b. Тогда они пересекаются в некоторой точке М. А так как по условию каждая из этих прямых параллельна прямой с, то получается, что через точку М проведены две прямые а и b, параллельные одной и той же прямой с. А мы знаем по аксиоме параллельности, что через точку вне прямой можно провести не более одной прямой, параллельной данной. Пришли к противоречию с аксиомой. Это показывает, что наше предположение о непараллельности прямых а и b неверно, следовательно, а||b, что и требовалось доказать.

  Другой пример.

  Теорема. Среднее арифметическое двух положительных чисел не меньше {значит: больше или равно) среднего геометрического этих чисел.

  Эту теорему можно так записать:

 , где а>0, b>0, (1)

  Ее можно доказать как прямым способом, так и способом от противного. Докажем ее способом от противного.

  Для этого допустим, что она неверна, т. е. среднее арифметическое меньше среднего геометрического двух положительных чисел: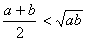;  (2)

  Умножим обе части (2) на 2 и возведем их в квадрат, получим: a² + 2ab + b²<.4ab или a² — 2ab + b² < 0. По формуле квадрата разности двух чисел получаем: (а — b)² < 0.

  В результате получили явную нелепость: квадрат некоторого числа (а — b) отрицателен, чего быть не может. Следовательно, предположение о неверности теоремы привело к противоречию, что доказывает справедливость теоремы.

  Таким образом, доказательство от противного некоторой теоремы состоит в том, что мы делаем допущение о неверности заключения теоремы. Затем делаем ряд логических умозаключений на основе этого допущения, в результате которых приходим к явно нелепому положению (к противоречию с условием или ранее доказанными теоремами, аксиомами). Далее рассуждаем так: если бы наше предположение было бы верным, то мы могли бы прийти лишь к верному выводу, а так как мы пришли к неверному выводу, то это означает, что наше предположение было ложным, следовательно, тем самым мы убедились, что заключение теоремы верно.

  Заметим, что если в результате рассуждений мы не получили бы нелепости (противоречия), то это еще не означало бы, что предположение верно. Иными словами, если исходить из верности (справедливости) заключения теоремы и из этого предположения получить верное (очевидное) следствие, то это еще не значит, что предположение верно: может случиться, что исходная теорема как раз неверна.

  На этом построены многие софизмы (умышленно ложно построенные умозаключения, кажущиеся лишь правильными), этим объясняются многие ошибки, допускаемые, при решении задач.

  Рассмотрим, например, такое равенство: а — b = b — a   (1), где а и b — произвольные числа. Допустим, что (1) верно, тогда возвысим обе части (1) в квадрат, получим:

  a² - 2ab + b² = b² - 2ab + a²

  Перенеся все члены в одну сторону и сделав приведение подобных, придем к совершенно верному равенству: 0 = 0.  Но отсюда нельзя делать вывод, что и исходное равенство (1) верно. Если бы мы такой вывод сделали, то пришли бы к такому софизму: 2а = 2b или а = b, т. е. любые произвольные числа равны между собой. Ошибка состоит в том, что из равенства квадратов двух чисел не следует равенство самих этих чисел. Например, (-2)² = 2², но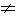 -22.

  Вот пример ошибочного решения задачи.

  Задача. Решить уравнение 3+ x + 2 = 0    (1).

  Допустим, что уравнение (1) имеет решение и, следовательно, равенство (1) верно. Тогда получим: З= — х — 2. Возведем обе части равенства в квадрат: 9х = х² + 4х + 4 или х² —5x + 4 = 0, отсюда x₁ =4, х₂=1. Можно ли найденные значения х считать корнями уравнения (1)? Некоторые ученики отвечают на этот вопрос утвердительно, ибо ведь все преобразования уравнения верные. И все же ни одно из найденных значений х не является корнем (1). Это подтверждает проверка. Подставляя найденные значения х в (1), получаем явно нелепые равенства: 12 = 0 и 6 = 0.

  А как все же решить это уравнение. Заметим, что выражение в левой части уравнения имеет смысл, если x0. Тогда левая часть уравнения при любых допустимых значениях х принимает только положительные значения и ни как не может быть равной 0, следовательно, данное уравнение корней не имеет.

  Таким образом вы должны учиться доказывать теоремы (формулы, тождества и т. д.), овладевать общими способами поиска доказательства теорем.

Перейти к следующей странице