Основные понятия тории множеств.

  Понятие «множество» в настоящее время — одно из основных понятий математики..

  Рассматривая какие-либо объекты (абстрактные или конкретные), можно в рассуждениях из всех или некоторых из них мысленно образовать новый объект: множество этих объектов. О последних тогда говорят, что они принадлежат данному множеству, или же, что они являются его элементами. Например, рассуждая об учениках какой-либо школы, мы можем ввести такие новые объекты, как множество учеников 4А класса, множество учеников, пропустивших занятия в сентябре месяце, и пр..  Рассматривая книги какой-либо библиотеки, можно  говорить о множестве книг по математике, множестве книг в картонном переплете, множестве книг по физике и т. д. В математике рассматривают  числа, точки плоскости, фигуры, функций и другие объекты. В этой связи мы говорим о множестве натуральных чисел, множестве четных чисел, множестве простых чисел, множестве, состоящем из чисел 2, 7, 1021, о множестве прямоугольных треугольников, множестве квадратов, множестве непрерывных функций, определенных на интервале (0, 1), и т. д.

  Дело здесь, конечно, не в словосочетании «множество таких-то и таких-то объектов», а в том, что это словосочетание вводит в рассмотрение новый объект, отличный от исходных, обладающих рядом специфических свойств. Так, например, конечное множество содержит некоторое определенное число элементов; из двух множеств А и В одно может быть больше другого; одно может содержать другое. Все это свойства множеств, а не свойства входящих в них элементов.

  Для отношения принадлежности принято пользоваться символом. Выражение аА означает утверждение «Объект а принадлежит множеству А» или «Объект а является элементом множества A».

  Для однозначного описания множества, образованного из каких-либо элементов, мы будем пользоваться двумя способами обозначения. Для любых объектов а₁, а₂, а₃,...,а_n множество этих объектов обозначается через

 {а₁, а₂, а₃,...,а_n}       (1)
(здесь в фигурных скобках перечислены обозначения всех названных элементов).

  Следует обратить внимание на то, что объект а и множество{a} - это различные вещи: первое - это объект, обозначенный через а, второе - это множество, состоящее из (единственного) объекта а. Отметим, что а{а} — истинное утверждение, между тем как {а}а — утверждение ложное. Другая форма обозначения состоит в указании общего свойства объектов, из которых мы образуем множество. Оно имеет вид:

  N = {x | P(x) },              (2)
Читается: «множество всех х таких, что Р(х)», где Р обозначает свойство, характеризующее в точности все элементы данного множества. Например, обозначает множество четных чисел, или

  M = {х | х — действительное число и х >}
- множество действительных чисел, больших числа. Такое обозначение множеств связано с так называемым принципом абстракции (или принципом свертывания), положенным в основу образования множеств создателем теории множеств Г. Кантором (1845—1918). Согласно Кантору, для произвольного свойства объектов мы можем образовать новый объект — множество всех объектов, обладающих данным свойством. Возможность перехода от формулировки свойства к множеству объектов, обладающих данным свойством, и есть принцип абстракций.

  Обе формы обозначений вполне естественны: для того чтобы указать какое-то определенное множество, нужно либо перечислить его элементы (что, строго говоря, возможно лишь тогда, когда таких элементов лишь конечное число), либо указать характерное свойство его элементов.

  Два множества считаются равными тогда и только тогда, когда они состоят из одних и тех же элементов.

  Это принятое в теории множеств положение называется принципом объемности (или принципом протяженности). Вместе с принципом абстракции оно указывает на существенную разницу между понятием свойства и понятием множества: одно и то же множество может быть определено различными свойствами.

  Равенство множеств M и N обозначаются M = N, а неравенство множеств через M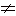N.

  Доказательство равенства каких-либо множеств А и В состоит из двух частей: в первой части доказывается, что если xB, то  xА, во второй части - что если
xB, то xA.

  Пример 1. Докажем, что множество А всех натуральных четных чисел равно множеству В, состоящему из всех натуральных чисел представимых в виде суммы двух натуральных нечетных чисел.

 Доказательство.

  Пусть xA, согласно условию это натуральное четное число, поэтому, найдется такое натуральное чило m, что x = 2m. Но 2m = 2m - 1 + 1 = (2m -1) + 1, это сумма двух нечетных чисел: 2m - 1 и  1. Таким образом  xВ. Мы доказали, что если xA, то xВ.

  Пусть xВ, согласно условию x равно сумме двух нечетных чисел, т.е. x = (2m + 1) + (2n + 1) = 2m + 1 + 2n + 1 = 2m + 2n + 2 = 2(m + n + 1), но это четное число и тогда xA. Мы доказвли, что если xВ, то xA.

 Множества А и В равны.

 Пример 2. Пусть даны два множества {2, 4, 6} и {4, 2, 6} Поскольку они состоят из одних и тех же элементов 2, 4, 6, то эти множества равны. Но ни одно из них не равно множеству {2, 4, 4, 6}, так как у элементов 4 и 4 должно быть как минимум одно свойство по которому мы эти элементы должны различать. Если таких свойств нет, то такая запись не допустима.

 Замечание. Пусть мы имеем множество равных между собой треугольников, у которых соответствующие стороны, углы, медианы, высоты, биссектрисы равны, но тем не менее мы их различаем либо по именам ABC, A₁B₁C₁,  A₂B₂C₂,..., либо по расположению на плоскости, либо по другим каким-то признакам.

Замечание. Ни каких ограничений на выбор элементов для вновь создаваемые множества не накладывается. Наверное поэтому иногда возможны неприятные ситуации.

 Например.

 Парадокс брадобрея. В некой воинской части командир приказал брадобрею, чтобы он брил только тех военнослужащих вверенной ему части, которые сами не бреются. Брадобрей добросовестно выполнил приказ, но когда он побрил всех самостоятельно не бреющихся перед ним возникла не разрешимая проблеиа брить себя или нет? Если он себя не бреет, то нужно брить себя. Если он себя бреет, то он брить себя не должен.

  В математике установление равенства двух множеств, полученных в результате абстракции двух существенно различных свойств, может оказаться трудной теоремой. Так, например, далеко не сразу видно, что множество простых нечётных чисел, которые можно представить в виде суммы двух квадратов, равно множеству простых чисел, дающих при делении на 4 остаток 1.

  Равно или не равно множество целых чисел, являющихся суммой двух нечетных простых чисел, множеству четных чисел, больших чем 2, до сих пор не решенный вопрос, известный как проблема Гольдбаха.

  Самое первое и самое важное свойство конечных множеств состоит в том, что каждому из них соответствует некоторый объект, называемый «числом элементов данного множества». Например, множеству пальцев моей левой руки, множеству диагоналей некоторого десятиугольника, множеству корней уравнения х² - 7x +6 = 0 соответствуют числа 5, 35, 2. Но что же это такое - число элементов какого-либо множества? Этот вопрос в науке до XIX столетия вообще не стоял. Когдато это понятиие считалось изначальным, врожденным. Знаменитый немецкий математик Кронекер (1823- протяжении многих сотен тысяч лет люди знали лишь количества, описываемые словами «один», «два», «много». Формирование же понятия «число элементов произвольного множества» — одно из величайших достижений человека, сравнимое по своему значению с изобретением письменности. И оно отнюдь не столь просто, как может на первый взгляд показаться в силу давней привычки к повседневному употреблению.

  Человек, даже не знающий чисел, тем не менее может сравнивать конечные множества, устанавливая для двух множеств М и N, содержат ли они одинаковое число элементов или одно из них содержит больше элементов, чем другое. Возможность такого сравнения представляет собой нечто, что предшествует понятию «число элементов некоторого множества». Сравнение осуществляется так: если, скажем, М — мешок с синими шарами, a N — мешок с красными, то для сравнения нужно, очевидно, сопоставить каждому синему шару один красный, образуя пары:

 "мешок" M:              

 "мешок" N:               

  Если при этом синие и красные шары одновременно исчерпаются, то сопоставление называется взаимно-однозначным соответствием между множествами М и N, а о множествах М я N говорят, что они равночисленны, или равномощны. Если же при сопоставлении некоторые элементы одного из множеств, скажем М, останутся без напарников, то о нем говорят, что оно содержит больше элементов, чем другое. Как видно, для количественного сравнения двух множеств числа не нужны и не обязательно уметь считать: понятие равночисленное предшествует понятию натурального числа. Все конечные множества можно мысленно рассортировать, относя в один и тот же класс все между собой равночисленные множества (так же как какие-либо предметы можно рассортировать по цвету, весу или еще по какому-нибудь свойству), и то общее, что присуще такому классу, и есть «число элементов любого множества данного класса». Например, 5 — это то общее свойство, которое имеют все конечные множества, которые равночисленны множеству пальцев  правой руки человека.

  Приведенное обоснование понятия натурального числа относится к конечным множествам: оно в неявной форме лежит в основе начал арифметики в младших классах школы. Такие рассуждения развивались и уточнялись на протяжении XIX столетия. Проблемы анализа побудили немецкого математика Г. Кантора в 70-х гг. XIX в. применить аналогичные идеи при рассмотрении бесконечных кардинальных чисел, обобщающих обычные натуральные числа. Мы должны на этом остановиться, несмотря на то что указанная тема находится несколько в стороне от традиционной «школьной» математики, так как ее разработка ознаменовала рождение теории множеств.

  В очень упрощенном виде исходные идеи Г. Кантора можно сегодня задним числом примерно представить так. Нельзя ли и бесконечным множествам приписывать «кардинальные числа», сопоставляя одно и то же «число» бесконечным множествам, между которым можно установить взаимно-однозначное соответствие? Ведь взаимно-однозначные соответствия устанавливаются в математике не только для конечных множеств, но и для бесконечных. После нескольких лет упорного труда его попытка осуществить эту идею увенчалась успехом.

  Чтобы уяснить себе, как возникли кардинальные числа бесконечных множеств, надо, очевидно, рассмотреть примеры взаимнооднозначных соответствий между бесконечными множествами, с которыми мы сталкиваемся в математике. Одно из самых первых бесконечных множеств — это множество N всех натуральных чисел:

  N = {1, 2, 3, ...},
и очень естественно попытаться сравнить именно это множество с рядом других бесконечных множеств.

  Рассмотрим, например, множество М всех натуральных чисел, больших 3. Оказывается, оно равномощно множеству N, что показывает нижеприведенное взаимно-однозначное соответствие:
N     1         2       3      4 ...       n ...
                              
М    4         5      6        7 ...   n + 3 ...

  Пусть Р — множество всех положительных четных чисел. Оно также равномощно множеству N, что показывает взаимно-однозначное соответствие n2n, которое каждому натуральному числу n сопоставляет четное число 2n.

  Больше того, множество N оказывается равномощным множеству Q всех положительных рациональных чисел. Для установленияэтого интересного факта воспользуемся схемой, предложенной Кантором. Выпишем все рациональные числа в виде бесконечной схемы: в первом ряду все целые положительные числа, во втором — последовательно все числа, со знаменателем 2, в третьем — со знаменателем 3 и т. д. (рис. 1). В этой схеме встретится каждое рациональное число (и не один раз, но это не страшно). Теперь выпишем все числа последовательно в том порядке (по диагоналям), как указано на рисунке 1, опуская каждый раз рациональное число, если равная ему сокращенная дробь уже встретилась, и подпишем под каждым числом следующее натуральное число. Легко видеть, что тем самым устанавливается взаимно-однозначное соответствие:

  Может показаться, что предложенное определение равночисленности кажется «слишком, хорошо» работает, так что все бесконечные множества между собой равномощны. Если бы так оказалось, то понятие кардинального числа для бесконечных множеств теряло бы всякий интерес: всем бесконечным множествам следовало бы приписать одно и то же кардинальное число «бесконечность». Тем более существенным оказалось открытие Г. Кантора о существовании, бесконечных множеств, не равномощных множеству N.

  Приведем его рассуждение. Покажем, что множество действительных чисел из интервала (0, 1) не может быть поставлено во взаимно-однозначное соответствие множеству N всех натуральных чисел. Заметим, что каждое действительное число из (0, 1) можно рассматривать как бесконечную десятичную дробь 0, а₁ а₂ а₃ а₄... а_n..., где разряды a а_t — это одна из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

  Предположим теперь, что нам удалось установить такое соответствие:

  10, a'₁ a'₂ a'₃ ... a'_n ...

  2 0, a''₁ a''₂ a''₃ ... a''_n ...

  30, a'''₁ a'''₂ a'''₃ ... a'''_n ...

  ...

  m0, a^m₁ a^m₂ a^m₃ ... a^m_n ...

  ...
что каждому натуральному числу k отвечает некоторое число
0,a^k₁ a^k₂ a^k₃ ...

  Тогда мы можем указать действительное число
b = 0, b₁b₂ ..., которое наверняка в этом списке не встречается. Цифры b_i числа b определим так:
b_i = 5, если i-я цифра аⁱ_i i-го числа не равна 5,
b_i = 9, если i-я цифра аⁱ_i i-го числа равна 5.

  Ясно, что b в предполагаемом бесконечном списке не встречается, так как оно отличается от каждого из чисел этого списка по меньшей мере одним разрядом: от i-ro числа в i-м разряде. Тем самым показано, что N и множество чисел на (0, 1) не равномощны.

  Итак мы получили пример двух неравномощных бесконечных множеств. Нетрудно показать, что существуют бесконечные множества, не равномощные ни множеству натуральных чисел, ни множеству действительных чисел из отрезка (0, 1). Следуя тому же принципу, который приводит в случае конечных множеств к натуральному числу, можно ввести в рассмотрение и бесконечные кардинальные числа, а именно говорят, что два множества. М₁ и М₂ равномощны, если между ними можно установить взаимно-однозначное соответствие. Это приводит к разбиению всевозможных множеств на классы равномощных. Тогда под мощностью, или кардинальным числом, следует понимать то общее свойство, которым обладают равномощные множества. Классы равномощных конечных множеств определяют таким образом обычные натуральные числа, бесконечные множества приводят к новым бесконечным кардинальным числам. Множества, равномощные множеству N натуральных чисел, называются счетными, им приписывается кардинальное число «счетное»; множествам, равномощным отрезку (0, 1), приписывается мощность «континуума»; как уже говорилось, есть и другие бесконечные мощности.

 
перейти на следующую страницу