Решение иррациональных неравенств.

 1. Достаточо часто при решении иррациональных неравенств после преобразований получаютлучают неравенство вида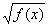>В этом случае обе части неравенства положительны и их можно возводить в квадрат. Возведение обеих частей в квадрат в общем случае позволяет получить неравенство, которое является следствием данного. Чтобы отсеять посторонниие решения находят ОДЗ исходного (данного) неравенства и находят пересечение этих множеств.

 Пример 1. Решить иррациональное неравенство.

 >

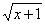
 Решение.

 1) Найдем ОДЗ.

 x + 10 и 20 - x0;

 -1x20, следовательно, ОДЗ - [-1; 20] (1)

 

 2) Возведем обе части неравенства в квадрат. 20 - x > x + 1;

 2x < 19; x < 9,5, следовательно решение этого неравенства (-; 9,5) (2).

 

 3) Найдем пресечение множеств (1) и (2), это будет множество [-1; 9,5).

 Ответ: [-1; 9,5)

 Можно поступить иначе, сразу заменить исходное неравенство системой неравенств и решать полученную систему неравенств.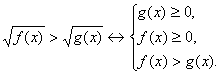
Заметим, что f(x) > g(x) и g(x)0, значит в силу транзитивного сойства неравенств, всюду, где выполняются указанные неравенства, f(x)0 и поэтому систему можно заменить другой системойтакая замен существенно упрощает решение иррационального уравнения.

 Пример 2. Решить неравенство>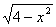

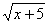
4 - x² > x + 5;
x + 50;


x² + x + 1 < 0;
x-5;

 Квадратный трехчлен x² + x + 1 имеет положительный старший коэффициент и отрицательный дискриминант, следовательно, он принимает только положительные значение, а это значит, что неравенство x² + x + 1 < 0; решений не имеет. Решение системы есть пустое множество.

 Ответ: x

  Пример 3. Решить неравенство

 Решение.

 Составим систему неравенств.

x³ + x² + x + 20,
x² + x + 1000,

x³ + x² + x + 2 > x² + x + 10;

 Так как первое неравенство является следстствие второго и третьего неравенств, его можно опустиь.

x² + x + 100,

x³ + x² + x + 2 > x² + x + 10;


x² + x + 100,
x³  > 8;

 У квадратного трехчлена a = 1 и D = -39, следовательно, он принимает положительные значени на всей области определения.

(-; +),

(2; +);

 Ответ: (2; +).

 2. Теперь рассмотрим уравнения вида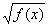> g(x). Поскольку левая часть неравенства может принимать как положительные так и отрицательные значения, то возводить без определенных условий обе части в квадрат нельзя. Мы должны рассмотреть два случая: g(x) < 0 и g(x) > 0, то есть неравенство равносильно совокупности двух систем неравенств.

 

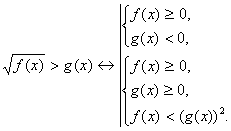
 Так как g(x) > 0, то (g(x))² > 0 и, в силу транзитивного свойства неравенств, во второй системе первое неравенство можно опустить.

 Пример 4. Решить неравенство> x + 1.

 1. Решим первую систему.

x + 30,
x + 1 < 0;


x-3,
x < -1;

 Решением этой системы является х[-3; -1).

 Решим вторую систему:

x + 30,
x + 10;
x + 3 > (x + 1)²:

x-1;
x + 3 > x² + 2x +1;

x-1;
x² + x - 2 < 0;

 У квадратного трехчлена x² + x - 2  a = 1, D = 1 + 8 = 16 > 0, x₁ = -2, x₂ = 1.

x-1;
-2 < x < 1;

  Решение второй системы x[-1; 1). Объеденив два полученных множества, получим множество являющееся решением иррационального уравнения х[-3; 1).

 Ответ: [-3; 1).

 3. Неравенства вида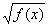< g(x). Из определения квадратного корня следует, что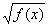0, поэтому g(x) > 0. Тогда

 

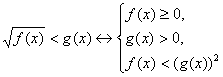
Неравенство g(x) > 0 в этой системе  опустить в общем случае нельзя.

 Пример 5. Решить неравенство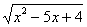2x - 2.

x² - 5x + 40,
2x - 20;
x² - 5x + 4(3x - 3)²;

x1 x4,
x1;
(x - 1)(x - 4)4(x - 1) ²;

x1 или x3,
x1;
(x - 1)((x - 3) - 4(x - 1))0;

x1 или x3,
x1;
(x - 1)(- 3x + 1)0;

x1 или x3, (1)
x1,                   (2)
x1 или x. (3)

 Ответ: {1}[4; +)

 4. Неравенство вида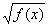+> m(x). Чтобы избавиться от иррациональности в таких неравенствах приходится несколько раз возводить в квадрат обе части неравенства, при этом мы должны учитывать, что возводить в квадрат обе части неравенства можно в тех случаях, когда обе части либо положительны либо отрицательны (в последнем случае необходимо менять знак неравенства). Нужно также учитывать, что при возведении в квадрат может произойти расширение ОДЗ, что приведет к появлению посторонних решений, их нужно отсеять.

  

 Пример 6. Решить неравенство-

 Решение.

 Найдем ОДЗ. Для этого нам необходимо решить систему неравенств.

x0,
10 - x0;
x - 50;

x0,
x10;5x10.
x5;

 Таким образом ОДЗ данного неравенства есть множество чисел принадлежащих промежутку [5; 10]

 Перенесем второе слагаемое в левую часть неравенства+, тогда при любом значении переменной из ОДЗ обе части положительны. Возведем их в квадрат.

 x + x - 5 + 210 - x;

 215 - 3x;

 В данном конкретном случае можно, по моему мнению, отклонится от стандартной схемы и вот почему. В правой части неравенства задана линейная функция t(x) = 15 - 3x, заданная на промежутке [5; 10]. Её угловой коэффициент k = -3, следовательно, она убывает и так как на концах промежутка она принимает соответственно значения t(5) = 0, t(10) = -15, то на указанном промежутке t(x)0. На этом же промежутке0 и0 (из определения квадратного корня), следовательно, на указанном промежутке неравенство 215 - 3x   верно при любом значении переменной из ОДЗ.

 Ответ: [5; 10].